• Resources
  • Directory
  • Webinars
  • CAD Models
  • Video
  • Blogs
  • EDGE Awards
  • Advertise
    • Ifd Electrical Engineer Scanrail Dreamstime 625ec825c5872
    1. Technologies
    2. Analog

    Frequency Quadrupler Enables Low-Frequency Measurements, Spans Up To Four Decades

    March 6, 2014
    The challenge in measuring low frequencies is that the counter gate time is often too short for the signal relatively long period. This non-critical circuit automatically multiplies an input single frequency times four to enable measurement of frequencies from 1 Hz to 40 kHz, tracking step changes in the input frequency as well. 

    This article is part of the Ideas for Design Series: Vol. 3, No. 2

    In frequency counters, the gating time allotted for counting is often too short to resolve low frequencies. A phase-locked loop could be used to multiply the input frequency. But in some cases, the signal changes too fast or too far for lock to be acquired or maintained.

    Related Articles

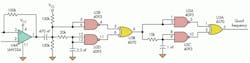
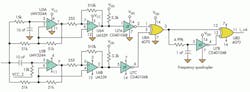
    To solve the problem, the circuit of Figure 1 is used to multiply the input frequency by a factor of four, spanning a range of 1 Hz to over 40 kHz, and it will track a step change anywhere in that range.

    1. The initial circuit implements ×4 multiplication for inputs up to 40 kHz to enable effective frequency counting despite short frequency-counter gating times.
    1. The initial circuit implements ×4 multiplication for inputs up to 40 kHz to enable effective frequency counting despite short frequency-counter gating times.
    There is one issue with this simple implementation, though. The constant delay at U2D (as seen at U3B output) tends to cause counting-by-twos in the lower decades (Fig. 2). 
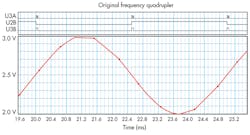
    2. The circuit’s shortcoming is a tendency to initiate counting-by-twos at the lower ranges, due to the fixed delay time of gate U2D.
    2. The circuit’s shortcoming is a tendency to initiate counting-by-twos at the lower ranges, due to the fixed delay time of gate U2D.

    A circuit that eliminates this issue provides a quadrature output over the frequency range (Fig. 3). Phase-lead and phase-lag circuits are used to create a constant 180° phase difference with respect to input frequency, at op-amp outputs (U5A and U5B).

    3. The addition of a quadrature function to the circuit changes the fixed delay time to a fixed phase difference, corresponding to variable time delay, overcoming the problem.
    3. The addition of a quadrature function to the circuit changes the fixed delay time to a fixed phase difference, corresponding to variable time delay, overcoming the problem.
    Connecting the comparator inputs U6A and U6B to the op amps U5A and U5B reduces the phase difference to 90°, as measured from one comparator output to the other. Constant phase means variable delay, overcoming the issue with the circuit.

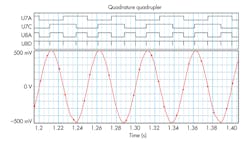
    Figure 4 shows the benefits provided by the quadrature circuit. The first XOR gate, U8A, produces the exclusive OR of the two quadrature outputs, U7A and U7C. This multiplies the input frequency by two. The second XOR gate, U8D, produces a pulse for each positive and negative edge of the signal from U8A, again multiplying by two. The result is four equally spaced output pulses at U8D for each cycle at the input.

    4. With quadrature and frequency multiplication by four at 20-Hz input frequency, the addition of the quadrature circuit clearly improves performance compared to the initial circuit.
    4. With quadrature and frequency multiplication by four at 20-Hz input frequency, the addition of the quadrature circuit clearly improves performance compared to the initial circuit.

    Quadrature maintains equal output pulse spacing as the frequency changes, so gating the pulse train will always count by ones. Quadrature is maintained within +0/–5° from 1 Hz to 49 kHz, but is lost above 49 kHz with the circuit values shown.

    Accurate tracking speed may be limited by the time required to acquire four output pulses at the new frequency from a step change to an accurate count, effectively a delay of 1/f seconds. This implies that accurate tracking is a function of the input frequency. Stepping from a higher to a lower frequency would require at least 1/flower seconds for the output to settle at four times the input frequency.

    The output pulse is set wide enough to be reliably captured by the processor or other counter input. If it is too wide, it will limit the upper frequency at which multiplication can be achieved. Too narrow, and the microprocessor or counter will miss counts.

    With the components shown, the output is a 5.6-μs pulse. This restricts the maximum theoretical multiplied output frequency to 89.3 kHz (input frequency less than or equal to 22.3 kHz). The quadrature circuit component values limit the maximum input frequency to 49 kHz or 196 kHz at the output of the multiplier. If the output pulse width could be made as short as 2.5 μs, the maximum multiplied output frequency would reach 196 kHz.

    Adjusting component values can move the usable range of multiplication higher or lower than that described here to fit the user’s requirements. With faster op amps, comparators, and logic components, the design might be able to perform at RF frequencies.

    Read more articles from the Ideas for Design Series: Vol. 3, No. 2

    Insidepenton Com Electronic Design Adobe Pdf Logo Tiny
    Download this article in .PDF format
    This file type includes high resolution graphics and schematics when applicable.

    Dave Conrad is a retired analog/digital hardware engineer who learned electronics by reading (starting at age 6) publications such as the ARRL Radio Handbook, QST, and CQ and later from various library books and Popular Electronics magazine. This was followed by a few courses in electronics in high school and junior colleges including TTL logic, along with learning on the job.

    About the Author

    David Conrad | Retired Analog/Digital Hardware Engineer

    Dave Conrad is a retired analog/digital hardware engineer who learned electronics by reading (starting at age 6) publications such as the ARRL Radio Handbook, QST, and CQ and later from various library books and Popular Electronics magazine. This was followed by a few courses in electronics in high school and junior colleges including TTL logic, along with learning on the job.

    Continue Reading

    Sponsored Recommendations

    Comments

    To join the conversation, and become an exclusive member of Electronic Design, create an account today!