It’s lazy of me I know, but I tar two distinct issues with my Schrödinger’s Nodes brush. And to be honest, there’s hardly a quantum-mechanical connection. But it makes for a good headline, so I’ll do my best to explain my reasoning.
I’m sure you’ve all heard of Schrödinger’s Cat. In the analogical world in which this creature exists, the essence of cat is boiled down to the single property of “aliveness.” This property can have two states: alive or dead. Now imagine that the cat is in a box that’s impervious to all our efforts to detect the states inside it. Schrödinger poses the simple question: How do we know whether the cat within the closed box is alive or dead?
In the real world, we assume it must be one or the other. In this particular quantum interpretation, however, Schrödinger posits that it is in both states—a superposition. It’s the act of opening the box that triggers the “collapse of the wave function” (feel free to Google that) and results in an observable cat that’s either alive or dead.
Now, if you never ever open the box, do you really care (except on felinitarian grounds) what state the cat is in? Well, if it’s really true that the states inside the box can’t somehow interact with the world outside, maybe so. But maybe there’s a secret tunnel out of the box and into the real world that you’re unaware of. Maybe the cat is alive and well inside the box, and is tweeting uncomplimentary things about you. Things are going wrong with your life—until you open the box, and all you find is a cat, looking all “what, me?” innocent.
This is an example of the general idea that the observer affects the observation. You don’t know what is going on inside the box if you don’t make an observation. When you do make an observation, you only know what goes on in that box when you make the observation. In this case, the cat hides its phone, and you’re none the wiser.
One common observation in our world of electronics is the probing of a node during an episode of fault-finding. What you observe when you probe a node might not be what is “actually” happening at the node when you’re not probing.
The classic example of this is where the input capacitance of the probe is enough to suppress some high-frequency instability. Every time you probe the circuit, it works fine. It’s only broken when you’re not probing it. The DC path to ground through the probe’s input resistor is another characteristic of the observation equipment that can make a circuit appear functional – sometimes for many minutes – if a dedicated bias path has been left off.
Is It Really Happening?
A related idea is Berkley’s Node, after George “Bishop” Berkley’s musing on whether, if no one was present in a forest when a tree falls, it will actually make a sound. Well, in circuits as in forests (and real life, for that matter), just because you’re not looking doesn’t mean something isn’t happening. The lesson: There can be nodes in your circuit that you ignore at your peril. If you never look at them, how can you be sure that they are doing what they are supposed to do?
The reason we don’t look is that we don’t even consider that they should be doing anything useful. The class of circuits that presents this issue that has dogged me for most of my working life is the active filter. This beautiful (indeed, Fantastic) beast is often constructed with a number of op-amps, yet we normally think of it as a block with one input and one output. But there are other trees in that forest…
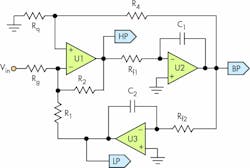
The state-variable filter circuit uses three op amps. (Courtesy of Wikipedia)
Consider the state-variable filter (see figure) as a Berkley’s Node example. This fine circuit is the Cadillac of 2nd-order (biquadratic or just “biquad”) filter sections; it uses three op amps when you cheapskates out there would just use one. Space limitations preclude an extensive discussion on why you would do this.
The key point is this: Consider the case where you just want a low-pass filter, not the additional bandpass or high-pass outputs. You build this circuit and take your filtered signal from the LP output shown in the figure. What could possibly go wrong? Well, quite a lot.
Here’s some homework for you. Fire up your favourite (I’m British, I spell that with a “u,” OK?) free simulator and “build” one. Use 10k resistors and 1-nF capacitors throughout, along with ”proper” op amps using sensible supply rails; let’s say ±5 V. Apply a 10-kHz squarewave (period of 100 μs, in other words) with a ±2-V amplitude (practical simulation hint: set the rise and fall times to something very low, like 1 ns; don’t just leave the field blank). How do the signals at the three op-amp outputs look?
Now increase that input signal amplitude. What happens if the amplitude exceeds ±2.5 V? What about increasing the input frequency—what else can go wrong? Hint: What input frequency would most provoke that undershoot?
Now do you see why you should be looking at the outputs you don’t want, as well as the one you do? I haven’t shown a graph, that’s your job. You need to burn your fingers on this one. Extra credit for sending me your thoughts .So here are two rules for you to remember:
- The Schrödinger’s Tweeting Cat rule: The behaviour (yep, we Brits use a “u” here, too) of an internal node may affect the performance of a circuit—until you observe (i.e., probe) it. So monitor the wanted output node of your circuit while probing internal nodes. This is how you’ll find that the oscillation that subtly disrupts the proper operation of your circuit only occurs when you don’t look for it.
- The Bishop Berkley’s Tree rule: In a circuit with N op amps, there are at least N nodes whose behaviours must be inspected during simulation, routine diagnostics, and fault-finding. This is how you’ll find that a node you thought was unimportant or uninteresting is actually clipping, or slew-limiting, or oscillating, or shorted to something by a PCB fault, or…
Those of you who are already members of that Burnt Finger Club will have your own stories about these phenomena. If you’d like to share them—or reminisce about something that happened in the past that now snaps into focus with these rules—comment below or let me know at [email protected]. Wait, what was that? Ah, no worries, just a tree falling on a cat…
About the Author
Kendall Castor-Perry
Senior MTS Architect, Programmable Systems Division
For nearly four decades, Kendall Castor-Perry has been chasing signals through electronic systems, wringing out the information they are hiding. He’s a world-class authority on filters and precision analog circuit engineering and a tireless champion of the needs of the customer. He has been widely published and syndicated, especially when sharing his extensive filtering knowledge as “The Filter Wizard.” He holds a BA in Physics from Oxford and an MBA in MBA stuff from London Business School. Kendall is currently Senior MTS Architect in Cypress Semiconductor’s Programmable Systems Division, pushing on the performance:power:price boundaries constraining tomorrow’s critical sensor-processing systems.