What’s the Difference Between Fixed-Point, Floating-Point, and Numerical Formats?
Download this article in PDF format.
Embedded C and C++ programmers are familiar with signed and unsigned integers and floating-point values of various sizes, but a number of numerical formats can be used in embedded applications. Here we take a look at all of these formats and where they might be found.
One reason for examining different formats is to understand how they work and where they can be applied. For example, fixed-point values can often be used when floating-point support isn’t available. Fixed point may be preferable in some instances, while floating-point support is available for other reasons, such as precision or representation.
Developers may be using single- and double-precision IEEE 754 standard formats, but what about 16-bit half precision or even 8-bit floating point? The latter is being used in deep neural networks (DNNs), where small values are useful. Small integers and fixed point can be used with DNN weights as well, depending on the application and hardware.
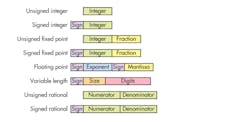
There are a variety number of ways to represent numbers. However, the layouts tend to vary only in the number of bits involved (see the figure). The use of the sign bit in binary-encoded values differs depending on whether 1’s or 2’s complement encoding is used. The 1’s complement approach uses the same encoding for the integer portion, which means there is actually a positive and negative zero value. A 2’s complement number has a single zero value, but there’s one more negative value than positive value. For example, an 8-bit signed integer includes values −128 to −1, 0 and 1 to 127.
Signed values have a single sign bit, but the other fields can vary in size depending on the implementation.
Defining the Options
Typical integer formats for microcontrollers and microprocessors include 8-, 16-, 32-, 64- and 128-bit values, depending on the platform. Many programming languages support different size integers that can be packed into structures or arrays. Peripheral interfaces may also need different size integers. Extending unsigned values to more bit is easy since all new upper bits are zero. A 2’s complement extension simply replicates the sign bit into the new upper bits. Detection of overflow is similar when reducing a value to fewer bits.
As noted, fixed-point formats offer an alternative to floating-point values. A fixed point consists of an integer and fraction portion. The number of bits used for each relates to the definition and implementation. Fixed point isn’t directly supported by programming languages like C and C++, although libraries are available that provide this support. FPGAs typically support fixed-point operations in addition to integer and floating-point operations. Floating-point support in an FPGA often uses more than 100 times as many gates compared to fixed-point support.
The integer portion of a fixed-point value is normally encoded in the same fashion as a signed or unsigned integer. The fraction portion is typically encoded for base 2 or base 10 representations. How the hardware and software handles this will vary. Some programming languages like Ada, MathWorks’ MATLAB, and National Instruments’ LabView have native fixed-point support.
Floating-point numbers have a mantissa and exponent. Most developers work with IEEE 754 standard floating-point formats that include three binary and two decimal formats. The binary versions are 32-bit single precision, 64-bit double precision, and 128-bit quad precision. The decimal versions include 64-bit and 128-bit versions. The exponent is a 2’s complement value for both formats. Binary and decimal versions vary with the mantissa value. The decimal standard supports densely packed decimal (DPD), which is more efficient than binary-coded decimal (BCD) that uses 4 bits for each decimal digit. BCD wastes almost 40% of the encoding possibilities compared to DPD.
IEEE 754 also defines positive and negative infinity values as well as NaN, or “not-a-number.” The other thing about the standard is that it defines more than just the encoding formats. It also specifies how operations are performed including corner cases.
Bits and Lengths
Using floating-point numbers that use less than 32 bits is common in a number of applications from graphics to machine learning. These smaller-format floating-point numbers provide the extended range of a floating-point number while being more compact in terms of storage. Oftentimes, larger formats waste space since the additional range or accuracy would not be useful.
The challenge of using smaller-format floating-point numbers is deciding how large of an exponent will be used. An 8-bit “minifloat” has a sign bit, a four-bit exponent, and three-bit mantissa. It supports infinity and NaN values. The largest value that can be represented is 1.875 * 217, or 245760. That’s somewhat more than the 128 supported by a signed integer.
Variable-length numbers are typically integers that vary in size versus the fixed-length formats already discussed. Normally, a size is included to specify the number of bits, bytes, or digits used by the digits field. Arithmetic operations take the size of the value into account. The advantage of this format is the ability to support very large numbers, which can be useful in many applications. Floating-point numbers can cover the range of this format, but not with the same precision since they’re limited by the number of bits in the mantissa.
Variable-length encodings can include different digit formats. The most efficient is binary, but BCD and even ASCII or EBCDIC has been used because strings are readily supported in most languages. The encoding density is even lower than BCD. However, storage efficiency and performance are often offset by other programming issues like ease of use and cross-platform data exchange.
A Rational Explanation
Rational numbers can be encoded as ratios of integer values. The integer values for the numerator and denominator can be a fixed size or variable length, depending on the support provided. Variable-length and rational numbers tend to be implemented by libraries. It’s possible to implement support in hardware using FPGAs.
The advantage of rational numbers over floating-point numbers is the ability to represent rational numbers like 1/3 without rounding errors. This can be useful in many applications; rational numbers are supported in a number of programming languages like Common Lisp, Haskell, Perl 6, and Ruby. Support in other languages is often available using libraries like the standard library ratio class in C++.
Of course, there are tradeoffs in performance and range compared to fixed- and floating-point representations. Use with transcendental functions can be a challenge.
About the Author
William G. Wong
Senior Content Director - Electronic Design and Microwaves & RF
I am Editor of Electronic Design focusing on embedded, software, and systems. As Senior Content Director, I also manage Microwaves & RF and I work with a great team of editors to provide engineers, programmers, developers and technical managers with interesting and useful articles and videos on a regular basis. Check out our free newsletters to see the latest content.
You can send press releases for new products for possible coverage on the website. I am also interested in receiving contributed articles for publishing on our website. Use our template and send to me along with a signed release form.
Check out my blog, AltEmbedded on Electronic Design, as well as his latest articles on this site that are listed below.
You can visit my social media via these links:
- AltEmbedded on Electronic Design
- Bill Wong on Facebook
- @AltEmbedded on Twitter
- Bill Wong on LinkedIn
I earned a Bachelor of Electrical Engineering at the Georgia Institute of Technology and a Masters in Computer Science from Rutgers University. I still do a bit of programming using everything from C and C++ to Rust and Ada/SPARK. I do a bit of PHP programming for Drupal websites. I have posted a few Drupal modules.
I still get a hand on software and electronic hardware. Some of this can be found on our Kit Close-Up video series. You can also see me on many of our TechXchange Talk videos. I am interested in a range of projects from robotics to artificial intelligence.