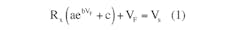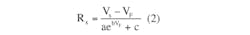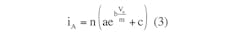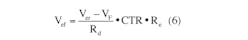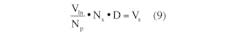Graphical, Numerical Techniques Size LED Array’s Drive

May 22, 2013

The nonlinear relationship between forward voltage and current in an LED makes it difficult to properly size the drive current and current-limiting resistor, but useful analysis can be derived from the exponential diode model.

Keng Wu

>> Electronic Design Resources
.. >> Library: Article Series
.. .. >> Series: Ideas for Design
.. .. .. >> Ideas for Design Volume 2

Download this article in .PDF format
This file type includes high resolution graphics and schematics.

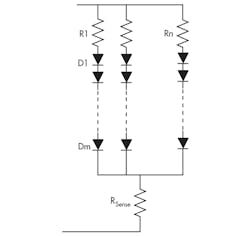
LED-based lighting is replacing incandescent and gas-discharge lamps in many situations. As practical lighting sources, and considering their directional nature, LED fixtures usually use multiple LEDs arranged in an array, with “m” LEDs in a serial string and “n” such strings in parallel (Fig. 1).

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 F1

1. Establishing the correct resistor size for each string of an array of n strings, where each strings has m LEDs, is challenging due to the nonlinear nature of the diodes.

For the array configuration and the exponential I-V characteristics model of a single LED,¹ it’s also possible to have a similar model representing the loading of such an array.

Related Articles

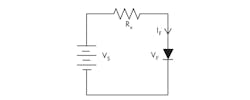
Since the single LED is a diode with a nonlinear forward-voltage/current, driving it with a fixed voltage source is generally not recommended. Rather, a serial (current-limiting) resistor is needed to equalize the power source and the load,(Fig. 2).

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 F2

2. Even for a single LED driven by a voltage source, the exponential current-voltage relationship complicates selection of the series-resistor value.

However, sizing this resistor requires a significant analytical manipulation. Using the single-LED exponential model, a Kirchoff’s voltage law (KVL) equation around the circuit loop gives:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq1

which can be rearranged to:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq2

where a, b, and c are model parameters for a selected LED, as defined in the reference.

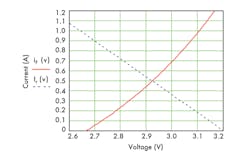
This is a challenge to solve symbolically, but it can be solved numerically with mathematical software tools. Alternatively, it can be solved graphically by separating the two key I-V relationship equations, v+ R_xI_F = V_s and I_F = ae^bv + c.

For example, using a Lumileds Luxeon Rebel ES LED with a 3.2-V dc source and a desired drive current of 0.5 A, the horizontal current line intercepts the LED curve at 2.92 V (Fig. 3). Therefore, the series resistor will be R_x = (3.2 – 2.92)/0.5 = 0.56 Ω.

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 F3

However, the graphical approach would not handle an LED array effectively, and the numerical method works better. To represent the array current i_A, the exponential model for the (m × n) array is modified, since voltage drops across current-limiting resistor R_n and sense-resistor R_Sense are usually small compared with driving-source V_s:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq3

With the array model, the switch-mode buck-regulating current driver in a closed-loop configuration (Fig. 4) can be described by a set of equations starting at the feedback point, circling around the control loop, and ending at the driver output:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 F4

4. Analysis of the switch-mode buck-regulating current driver in a closed-loop configuration for driving an array yields a set of equations that are better solved using numerical computation rather than an analytical, closed-form approach.

• Current sensing:

V_f = i_A • R_Sense(4)

• Error amplifier:

V_er = A(V_Ref – V_f) (5)

• Effective error:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq6

• PWM ramp:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq7

• Duty cycle, D:

V_Ramp(D • T_s) = V_ef(8)

• Power stage:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq9

With effort, all the equations can be consolidated into a single, closed-loop equation:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 05 Ifd2551 Eq10

This is a transcendental equation with an exponential term that prevents us from solving it analytically, but it can be solved using computational techniques and software tools.

Reference

1.“Generate Realistic Models for LED Current Versus Voltage” Keng C. Wu; Electronic Design, Vol. 61, No. 1, p. 52, Jan. 10, 2013, http://electronicdesign.com/power/generate-realistic-models-led-current-versus-voltage