Engineers involved in high-speed digital communications are all comfortable observing and analyzing signals and systems as a function of time. We live in the time domain. Signals and systems are also characterized as a function of frequency. This is an area where RF/microwave engineers are most comfortable. As communications speeds move well into the gigabit/s regime, digital engineers need to learn how frequency domain measurements provide valuable insights into time domain behavior. Similarly, RF/microwave engineers are being pressed into service as signal integrity engineers in digital applications. Time-domain measurement skills are required.
This file type includes high resolution graphics and schematics when applicable.
Table Of Contents
• The Importance Of The Time/Frequency Domain Relationship
• Relating Time-Amplitude Distortions To Frequency Effects
• Network Analyzer Measurements
• The Time Domain Transmission Test
• Transmission Line Measurements Using Time Domain Reflectometery
• The Effect Of Jitter And Phase Noise
• Summary
The Importance Of The Time/Frequency Domain Relationship
Electrical engineering students rarely leave college with knowledge depth in both digital electronics and RF/microwave theory. The new engineer with digital design skills likely chose that path from a desire to be a part of the world of computers. The high-frequency engineering student often has a love for radio communications that preceded entry into college.
A typical electrical engineering degree typically includes some coursework in both digital electronics and RF/microwaves. But when it came time to specialize and choose course electives beyond the basics, and an anticipated career, there was likely a distinct fork in the road. One path led to the world of Boole and Karnaugh, the other to Maxwell and Smith.
Related Articles
- User-Configurable FPGAs Unlock Test Instrumentation
- Understanding Intermodulation Distortion Measurements
- What's Inside Your RF Signal Analyzer?
For many engineers, as their careers have progressed, those paths have begun to merge. As common computer serial busses reach 2-, 5-, and even above 10-Gbit/s transmission rates, it is easy to argue that the digital and RF/microwave worlds are converging. What does this mean for microwave engineers?
Even though simple ones and zeroes are being transmitted, skill with transmission lines, noise processes, phase-locked loops (PLLs), and communications theory become critical for successful digital communications system designs. For the digital engineer, knowledge of digital logic, data encoding, error detection, and recovery is still essential. Rather than dealing with security applications or data corruption caused by imperfection in storage media, these skills now are applied to communications schemes where the transmission channel, used at high speeds, can degrade signals even though the transmitter and receiver may be separated by a fraction of a meter.
What can suit the high-frequency engineer better for a digital communications world? Similarly, what can make a digital engineer more effective when “bits” include microwave signal content? The ability to think in both the time and frequency domains allows both engineers to thrive in each other’s world.
Observing a digital bit stream on an oscilloscope with some intuition about its frequency domain equivalent can provide valuable insights into the integrity (or lack of integrity) of that signal. Measuring the frequency response or bandwidth of a communications channel and anticipating how the shape of bits (in time) will be affected can help in understanding the viability of that channel.
An electrical signal can be displayed as a voltage versus time waveform. This is how signals are observed on an oscilloscope. The same signal also can be displayed in a power versus frequency format. This is what would be displayed on a spectrum analyzer.
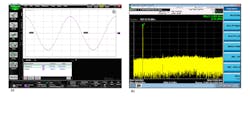
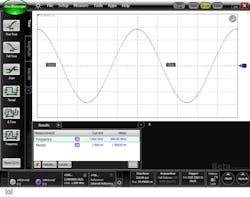
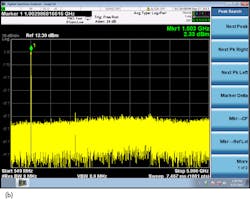
Mathematically, time and frequency signals are related by the Fourier transform. The Fourier transform takes a signal/function from the time domain into the frequency domain. It indicates what frequencies are present in a time domain waveform. Consider a sine wave with a period of 1 ns (Fig. 1a). What frequencies are present in this signal? This one is simple. There is only one frequency present, a single tone at 1 GHz (Fig. 1b).
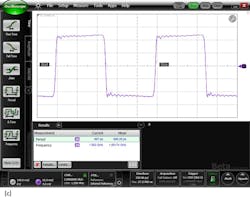
What about a square wave with a period of 1 ns? One would expect that it will also have signal content at 1 GHz. But obviously there is more spectral content to this signal than the sinusoid with the same period. In addition to the tone at 1 GHz, there is energy at 3 GHz, 5 GHz, 7 GHz, and so on (Figures 1c and d). The signal comprises a tone at the fundamental rate (the inverse of the signals’ period) and its odd harmonics. But as the harmonic tones get higher in frequency, the amplitudes get lower.
As time domain signals become more complex, so is their spectrum in the frequency domain. For example, a digital data stream at 2 Gbits/s will have a spectrum that follows a (sin x)/x function, and, in contrast to the examples above, it will have no signal content at 2 GHz or harmonics of 2 GHz (Figures 1e and 1f). Note that the 1-GHz square wave is the equivalent of a 2-Gbit/s signal transmitting a 1-0-1-0-1-0 pattern, and the spectral nulls for the square wave and “real” digital communications are identical.
It is also possible to determine the time domain response of a signal when its frequency components are known—that is, the frequency spectrum of a signal can be used to determine the amplitude versus time waveform. This is achieved through the inverse Fourier transform. All the examples of Figure 1 apply. If the frequency spectrum is known (rather than the time waveform), the time waveform can be determined. Although not shown in Figure 1, phase information is required for an accurate reconstruction.
Relating Time-Amplitude Distortions To Frequency Effects
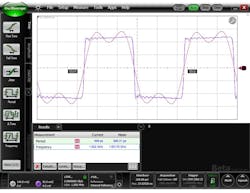
When digital data is observed on an oscilloscope, one could expect a series of nearly rectangular pulses representing logic ones and the absence of a pulse representing logic zeros. It might be surprising when a very high-speed digital signal is observed. The logic ones are not so rectangular. Even the logic zeros may not be flat lines at the zero-level amplitude. Instead, signal edges may have distinct slopes that consume a significant portion of the pulse duration or bit period. After a signal makes the transition from a zero level to a one level, it might overshoot and oscillate before settling to a final level (Fig. 2).
Basic filter theory can help explain some of the reasons behind these less than ideal data waveforms. When a filter is designed, the primary objective is usually to pass a specific range of frequencies while rejecting a certain range of frequencies. Given the discussion above regarding the relationship between the frequency content of a signal and its time domain characteristics, it should be clear that passing a waveform through a filter will likely alter its shape. Anytime the frequency spectrum of a signal is altered, its time domain performance will be altered too.
Consider the spectrum of the 1-GHz square wave of Figure 1d. What if that signal was transmitted through a low-pass filter that passed signals below 2 GHz and suppressed frequencies above 2 GHz? The only spectral element remaining would be the 1-GHz tone. The square wave becomes a sine wave. What if the filter passed frequencies below 4 GHz and rejected frequencies above 4 GHz? Now the signal comprises a 1-GHz tone and a 3-GHz tone. The signal will not be a 1-GHz sine wave, but it also cannot be the original 1-GHz square wave.
Figure 3 shows the effect of passing the square wave through the low-pass filter. Note how the rise time and fall time of the edges have been slowed down. Note also that there is some peaking and droop in the tops and bottoms of the pulses. In fact, the signal looks a lot like a fast sine wave (the 3-GHz tone) riding on top of a slower one (a 1-GHz tone). The filter is doing its job.
These examples were pretty simple. In practical filter designs, this will not be the case. Several issues must be considered:
• Will frequencies passed by the filter all experience the same propagation delay? If not, how will this affect the time waveform?
• Will signal spectrum in the pass band all experience the same level of attenuation? Some filter designs have ripple (varying attenuation) in the pass band. Others have peaking (a small region of amplification) prior to rolling off. How will this affect a time waveform?
• Remember, if the spectrum of the signal is altered, either by attenuation, amplification, or altering the phase relationship between the spectral elements of the signal, the waveshape will change. Is the waveform distortion acceptable?
When a filter is designed, it is important to know if time domain or frequency domain characteristics have priority. Some filters provide excellent frequency suppression at the expense of waveform distortion.
Consider that a digital communications system is working properly when the receiver can correctly interpret ones as ones and zeros as zeros. A mistake is known as a bit error. System performance is commonly described as the bit error ratio (BER), how many bits are received in error compared to the total number of bits received. Typical values are in the range of one error for every trillion bits transmitted.
A low BER is usually achieved when there is significant separation between logic 1 and logic 0 levels, as well as when logic decisions are made “far away” in time from where transitions from a logic 0 to a logic 1 (or vice versa) take place. The “decision point” is usually located in the middle of the bit (time wise) and halfway between the logic 1 and logic 0 levels.
If the signal deviates from ideal and is ever close to the decision point, the chances increase that a bad decision will occur. So when bit shapes deviate from ideal “rectangular” waveforms, BER is potentially at risk. In very high-speed digital communications networks, waveform distortion is often due to the spectrum of the signal being altered as it passes through the system. These filter concepts can be extended to the high-speed digital communications system.
An easy place to find a source of waveform distortion is the communications channel. The channel can be any media that carries the signal from the transmitter to the receiver such as a copper trace on a printed-circuit board (PCB), a metallic cable, or a strand of optical fiber. Most channels have some form of low-pass filter characteristic.
Several mechanisms attenuate very high-frequency signals as they propagate along a signal. In PCB traces or metallic cables, this can be due to dielectric materials having higher loss at high frequencies than low frequencies. High-frequency signals have a tendency to travel in the outer regions of a conductor rather than through the entire cross section of a cable. The effective conductivity is reduced, increasing attenuation.
Attenuation of the high-frequency spectrum of a digital signal can have an effect similar to what was seen when a square wave was sent through a low-pass filter. Rising and falling edges are slowed. For an optical fiber, high-frequency loss can occur when the light carrying the digital information travels a variety of path lengths, as there can be several simultaneous modes (paths) of propagation down the fiber. Digital information, propagating as pulses of light, will then arrive at the receiver dispersed in time. The dispersed pulses of light have characteristics similar to an electrical pulse that has been low-pass filtered. Edge speed is reduced, and the shapes of the pulses are changed. Again, as the quality of pulses degrades, the likelihood of bit errors increases.
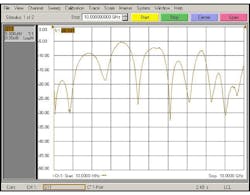
The most accurate way to characterize an electrical channel’s ability to carry high-frequency signals is with an instrument called a network analyzer. The network analyzer will inject a sine wave into the channel and measure the sine wave that comes out the other end. The output to input ratio is an indication of the loss through the cable. If the sine wave is swept over a broad range of frequencies, the attenuation characteristic of the cable over that frequency range can be determined.
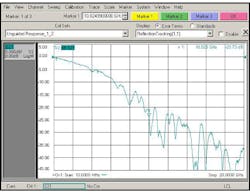
Figure 4 shows a network analyzer measurement of a signal path through a 25-cm length of copper trace on a common PCB. Note that at low frequencies, there is virtually no attenuation. But as the frequency of the signal increases, so does the attenuation. So what does this indicate about how this channel can or cannot be used in a high-speed digital communications system? Recalling filter theory, the cable frequency response is in some ways similar to the low pass filter. Low frequencies pass almost unaffected and high frequencies will be attenuated. The transmitted bits will be altered as they pass through the channel. How will they be altered?
There are a few different approaches to take here. The cable frequency response could be mathematically transformed into the time domain through the inverse Fourier transform. This would yield the impulse response of the channel, and it can indicate how a very narrow pulse is spread in time and reduced in amplitude. The ideal impulse signal has zero width in time. In the frequency domain, this implies an infinite bandwidth. As an ideal impulse passes through the channel, the high-frequency content is suppressed.
Back in the time domain, as the signal exits the channel, the effect of losing high frequencies is the spreading of the impulse. The rise and fall times are slowed down. How will this affect communications quality? Recall that if there is not a wide separation between the logic 1 and logic 0 levels, the receiver at the end of the channel is more likely to make a mistake when trying to determine what the level of a bit is.
What is the effect of a pulse spreading out in time? If the spreading is severe enough, energy from one bit can spill over into the slot allocated for the adjacent bits. This is a phenomenon known as inter-symbol interference (ISI), and it is another possible reason for a receiver to make a mistake.
At this point, it might seem reasonable to dispense with the network analyzer and simply inject a real digital communications signal and directly observe the quality of the bits on a high-speed oscilloscope as they exit the channel. This can be and often is done. However, communications systems often can be specified by their individual components such as the transmitter, the channel, and the receiver since the components of the communications system may come from different vendors. Each component must be specified in a standalone fashion. The frequency response measurement with a network analyzer achieves this for the complete channel.
The Time Domain Transmission Test
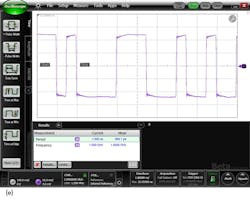
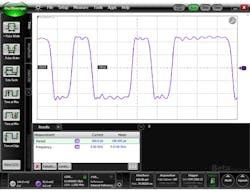
An alternative but related technique for characterizing a channel is to inject a very fast step pulse into the channel and observe with a wide-bandwidth oscilloscope the pulse that exits. Comparison of the output to the input indicates how a channel will degrade digital bits. This technique is called time-domain transmission (TDT).
Figure 5 shows the TDT response of the channel that was previously measured with the network analyzer seen in Figure 4. The input signal is seen in the blue trace. The step, after having traversed the PCB, is seen in the red trace. (Actual time delay between input and output is reduced to allow easier comparison of the changes in the edge speed). This is not the impulse response of the channel, but rather the step response.
However, similar results can be observed. If the channel were ideal, the output step would appear identical to the input step, but delayed in time due to the path length of the channel. But like the impulse response, high-frequency attenuation of the channel slows down the edge speed because the channel has attenuated the high-frequency components of the signal required for a fast edge.
The TDT response can be transformed into the frequency domain to show the frequency response of the channel. This capability can be built into the instrument so it can provide results similar to the network analyzer. Thus, the network analyzer and the TDT oscilloscope both can provide results in both the time and frequency domains through “native” measurements as well as transformed results.
Transmission Line Measurements Using Time Domain Reflectometery
The microwave engineer knows that when energy propagates along a transmission line or channel, it is very difficult to have the receiver absorb the entire signal. If the energy is not absorbed, it has to go somewhere. In most cases, the residual signal is reflected back in reverse direction along the transmission line.
This presents two problems. First, with less signal available to the receiver decision circuit, the chances that the receiver will make mistakes and degrade the BER increase. Second, the reflected energy will possibly return to the transmitter, and if the transmitter cannot absorb the reflected signal (it may not have been designed to do so), the signal can be re-reflected and travel back to the receiver. The receiver will now be seeing two signals, and they are often in conflict. The main signal can be degraded if it is a logic 0 and a “ghost” logic 1 is added to it. Similarly, a logic 1 with a logic 0 “ghost” added to it will be degraded from the ideal. In both cases, the separation of ones and zeros will be reduced and the chance of receiver errors will increase.
This leads to another measurement technique from the microwave world that is becoming increasingly important in digital communications. The ability to determine how a signal travels from the transmitter, through the channel, and to the receiver and whether any signal is reflected in the reverse direction from the receiver is critical. A reflection will occur anytime there is a change in the impedance of the signal path.
If a transmission line has a characteristic impedance of 50 Ω, and the receiver has an impedance of 60 Ω, about 9% of the voltage reaching the receiver will be reflected. Reflections can also be generated along the channel. Changes in trace widths, through holes and vias, dielectric changes, or anything that can cause the impedance to change, will result in a signal reflection.
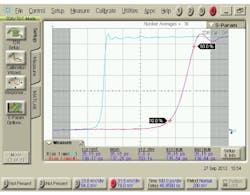
Again, the microwave engineer has relied on the network analyzer to characterize reflection performance. In this measurement, a signal is injected into the test device, perhaps a cable or an integrated circuit, and a directional coupler is used to extract and observe reverse traveling signals. The magnitude of the reflected signal is compared to the injected signal. The result is called return loss, and if the injected signal is swept over a range of frequencies, the return loss versus frequency is determined. Typically, as frequencies get higher, impedance becomes more difficult to control, and reflections increase.
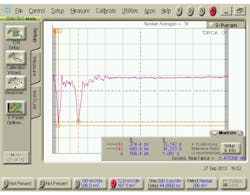
A similar time domain measurement is also available. Based on a wide-bandwidth oscilloscope, it is called the time-domain reflectometer (TDR). The instrument is essentially identical to the TDT. However, rather than measure the step pulse entering a device and exiting the opposite end, reflected signals are measured at the same port as the input signal. While the network analyzer displays reflections versus frequency, the TDR displays reflections versus time.
If the propagation velocity is known, the TDR effectively functions like radar. By knowing when reflections (echoes) return to the oscilloscope, the position of the reflection site can be precisely determined. The magnitude of any reflection is directly related to the impedance. The TDR then can display impedance versus position. Figure 6 shows a TDR display of a 50-Ω transmission line where the impedance drops to 33 Ω, returns to 50 Ω, drops to 33 Ω, and returns to 50 Ω.
It is interesting to compare the network analyzer return loss measurement with the TDR impedance measurement, particularly when there are multiple reflection sites. For the TDR, the impedance profile shows each location where impedance has changed. When the TDR trace steps up, the impedance has increased in that location. Where it steps down, the impedance has decreased.
How does the same device look when it’s measured with the network analyzer? Recall that reflection versus frequency is displayed. There is no direct indication of where reflections occur, or even if there is more than one reflection site. Whether there is one reflection site or more, the display is of the totalreflected energy versus frequency.
An interesting phenomenon can occur when there are two or more impedance discontinuities that are larger than all others. If there are two reflections, two signals will return toward the instrument. Because the signal from the reflection site that is farther out will have traveled farther than the first reflection, there will be a phase shift relative to the first reflected signal. The two reflected signals will combine in phase, 180° out of phase, or somewhere within ±180°. The phase relationship will depend on the distance between sites, the propagation velocity, and the frequency of the signal.
Because the frequency of the test signal is typically swept over a wide range, perhaps 50 MHz to 20 GHz, the two reflected signals will likely go in and out of phase with each other as frequency is increased. When the two reflected signals are completely out of phase, the total signal will become small (zero if the two signals are of equal magnitude). When the signals are in phase, the total will reach its maximum.
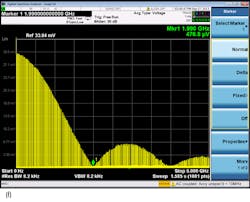
The resulting return loss display will vary from high to low versus frequency (Fig. 7). Although the frequency domain display of the network analyzer cannot directly indicate the presence of multiple reflections, the systematic high and low pattern in the frequency domain is a common indicator that there are at least two reflections that dominate the overall response.
The network analyzer vertical display is in decibels. In the worst case, the reflected signal power is 5 dB lower than the transmitted signal, or about 32% of the transmitted signal. The reflected voltage is actually more than half the original transmitted signal. This occurs when signals from the two reflection sites combine in phase. Maintaining impedance is essential to low-BER digital communications!
In the cases where the two reflections combine out of phase, the total reflected signal power is as low as 30 dB (0.1%) below the original transmitted signal. The reflected voltage is 3% of the original. The Fourier transform allows the network analyzer display to show the time domain response similar to the TDR and the TDR to display the frequency domain response, similar to the network analyzer.
The Effect of Jitter And Phase Noise
Jitter occurs when the edges of a bit stream do not occur at their expected locations in time, but instead are advanced or delayed. As data rates increase, one of the biggest problems being encountered is making sure that the receiver does not try to make its logic decision when the incoming signal is changing state. If a decision is made near a signal edge, BER is likely to increase. So, jitter is a source of degraded BER.
What will cause jitter? There are several mechanisms, and once again some lessons from the world of the microwave engineer can help. A reference clock usually governs the rate at which a transmitter sends out bits. If that clock does not operate at an exact frequency, the transmitted data will be sent out at a varying rate.
While the digital engineer calls this jitter, the microwave engineer may have called it phase or frequency modulation. In this case, it is an undesired modulation. The microwave engineer’s instincts would be to examine the clock in the frequency domain. Earlier it was shown that if the clock were an ideal sinusoid, a single tone would be observed in the frequency domain. If the clock were a square wave, the fundamental tone and its odd harmonic would be present.
What if the clock were a sinusoid that was varying slightly in frequency? This is actually very common. No oscillator can produce a pure tone. Internal electronics will always have some noise present, and this noise will cause a random fluctuation in the oscillator frequency. The random fluctuation is observed as a spreading of the spectrum, centered at the expected frequency. The microwave engineer would call this phase noise. The rate at which phase changes (frequency) has a random component to it.
The digital engineer, accustomed to viewing signals on an oscilloscope, would see edges that are misplaced in time in a haphazard fashion. Rather than calling it phase noise, the digital engineer would call it random jitter. These are two ways of describing the same thing, one from a time domain perspective, the other from the frequency domain.
Jitter can also occur in systematic ways. The ISI phenomenon discussed earlier is a jitter mechanism as well. Recall that it causes pulses to spread. If the pulse edges are moving outward in time from their ideal positions, causing energy to spill into adjacent bits, it is a jitter mechanism.
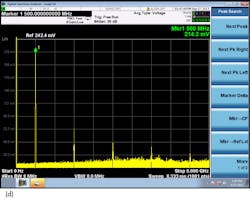
Additionally, jitter can be periodic. If the transmitter clock has a poorly regulated switching power supply, the switching rate can modulate the frequency. In the time domain, this is periodic jitter. In the frequency domain, it is frequency modulation. In the time domain, it is difficult to observe this directly. The effect is likely spread across thousands, even millions of bits. In the frequency domain, the effect sticks out like a sore thumb. When a signal is frequency modulated, tones or sidebands are easily observed, above and below the clock tone frequency, offset by the frequency of the switching (modulating) signal.
The ability to examine high-speed signals in both time and frequency provides valuable insight into root causes of good and bad performance. Each perspective has its strengths and weaknesses. As data rates increase, every engineer involved in high-speed digital communications systems can benefit from the ability to operate comfortably in both domains.
Greg Le Cheminant is a measurement applications specialist for digital communications analysis products in the Oscilloscope Products Division, Electronic Measurements Group, at Agilent Technologies. He is responsible for product management and development of new measurement applications for the division’s digital communications analyzer and jitter test products. He also represents Agilent on several industry standards committees. His 29 years of experience at Agilent and Hewlett-Packard includes five years in manufacturing engineering and more than 24 years in various product marketing positions. He is a contributing author to four textbooks on high-speed digital communications and has written numerous technical articles on test related topics. He earned BSEET and MSEE degrees from Brigham Young University. He holds two patents as well.