This time I’ve opened up the way-back machine and unearthed a piece I first published nearly 20 years ago, when I was at the Burr-Brown Corporation. Op-amp compensation is still a topic that surfaces regularly, so I thought revisiting it would surely be timely. I couldn’t locate it on the web—it was originally printed in a paper magazine. But an old backup hard drive yielded a hackable copy. So, sans the commercial puffery (I was trying to sell Burr-Brown op amps, after all) and with judicious editing, here is a classic 20th Century example of Castor-Perry technical outreach!
Ahh, 1999, Happy Days...
Nowadays it’s all websites and PDF files, but when I was a young engineer the Databook was a source of knowledge and inspiration in analog circuit design. I felt that these were books designed to make you feel good about circuit design and the wonderful world of components, especially that sine qua non of the analog designer’s art, the op amp.
Then one day I chanced upon the datasheet of an amplifier that, as one of the bullet points proudly displayed on the front page, boasted a Minimum Stable Gain of 5. The beginnings of a strange chill passed over me: Was this good? They must think it important to give it such prominence, and yet, it did sound rather like a warning, like “Maximum Occupancy: 35 Seated, 25 Standing” on a bus.
My colleagues weren’t able to help me out in my time of confusion. What if I were to use it in a circuit with a gain of x4.9? x4.8? Would it work?
Would it fail 2% of the time? Which 2%? Help!!
The manufacturers must have realized that these were not very easy products to sell. They tried changing the language used on the datasheets; the term “decompensated” cropped up more often but probably frightened even more people off. Most recently, the more need-focused “optimized for higher-gain applications” has appeared. However, there doesn’t appear to have been a concise treatment anywhere in the quality press, and so now a whole new generation of engineers is unsure about what this means and what the implications are for them. I’ll try to help with this article.
It’s All in the Feedback
This isn’t the place to reprint a couple of textbook chapters on feedback theory, but—and I do feel sorry for those of you who don’t care for equations and complex algebra—feedback is what this is all about. Books such as The Art of Electronics are essential reading for those designing with op amps. However, they don’t contain any material that tells you what happens when you play “hardball” with this Minimum Stable Gain issue. Nor do they enlighten one on the continuum between op amps that have some specified Minimum Stable Gain and those that do not.
In all important applications, op amps are used with some form of feedback network. This causes the input voltage applied between the two active input pins to be a function of both the input and output voltages.
From an engineer’s perspective, the ideal op amp is one that can be dropped into any circuit, allowing them to operate under real-world conditions without any “behavior” due to individual characteristics.
Why Op Amps Are Built the Way They Are
An op amp is an amplifier circuit made from several stages, each of which contributes to the overall voltage gain and to the isolation of the output circuit from the input connections. Each of these gain stages has a finite bandwidth, meaning that above a certain frequency, the gain starts to reduce. But more critically, the output begins to lag behind the input—there’s a phase shift between input and output.
Now for feedback to be “truly” negative—the most useful kind for the analog designer—the phase shift between the output of the op amp and the input to which the feedback is returned should be 180°. At higher frequencies, the extra phase lag introduced due to the finite bandwidth of the stages of the op amp reduces the “negativeness” of this feedback.
And woe betide us if we were to pick up an extra 180° of phase lag at a frequency where the overall response still shows some gain—because now we’d have positive feedback. In that case, a small change occurring at the input doesn’t cause an output change that tends to cancel it—the change tends to reinforce it.
In a practical circuit using such an amplifier with feedback, what then tends to happen is that the output voltage streaks away from where you’d expect it to be and generally doesn’t stop until constrained by clipping at the supply voltage. At this point, the output can’t change any more for any change of input voltage, so the gain disappears and so does the phase lag. As a result, the output now careens off toward the other supply rail.
Such full-scale oscillation is characteristic of the instability caused by applying far too much feedback around an amplifier. As we will soon see, there are less drastic manifestations where the oscillation isn’t continuous but dies away slowly, just making the output take a lot longer to follow the desired signal accurately.
Anyone who’s tried making high-performance amplifiers out of individual transistor gain stages knows how thorny this problem is. The concept of a practical op amp includes a fundamental aspect intended to address this and make the op amp into the easy-to-use, friendly component we all crave. That aspect is compensation.
Earlier, we imagined the op amp as a cascade of several stages, each of which added some phase lag. If one of these stages “cuts off” at a much lower frequency than all the others, then the amount of phase lag introduced does increase, but only up to a limit of 90°.
While this might still sound bad, in fact when we try it, we find out one of the magic pieces of op-amp theory. As long as you just have one of these phase lag stages—we call it a “dominant pole”—the amplifier circuit behaves impeccably; however, much feedback is applied around it. In other words, dominant pole compensation involves tweaking the amplifier design so that, for all practical purposes, you can ignore the presence of the other sources of phase lag.
The actual frequency at which the open-loop gain of the amplifier starts to roll off is not well defined, because it depends on the actual value of dc open-loop gain. So, the way we describe the effect of the first “pole” in the system is to describe the frequency at which the open-loop gain (strictly, its modulus) becomes unity. This is called the unity-gain crossover frequency, and it has the same value as the “gain-bandwidth product” for this simple type of amplifier, which we will call a “single pole” op amp.
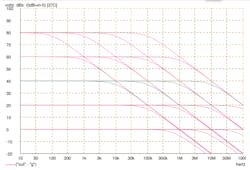
Figure 1 is a busy little graph showing the performance of four different op amps at five different closed loop gains. The op amps have a “perfect” single-pole response set to provide a unity-gain crossover frequency of 1, 10, 100 and 1000 MHz.
1. Four different “perfect” single-pole op amps at five different closed-loop gains.
These four responses are often realized by the same circuit by just changing the value of one capacitor. That capacitor is called the “compensation” capacitor and the amplifier is said to have “dominant pole compensation” if all other roll-offs occur at high-enough frequencies whereby they can be ignored. The inset box starts with a proof that, with this simple single-pole open-loop response, the response is a pure first-order lowpass response for any closed-loop gain.
Things are usually not this simple. If we set our sights for circuit bandwidth high enough, we may not be able to ignore the contribution of the other stages in the amplifier. Our dominant pole might only be “quite dominant,” and then we’ll be operating in a region between perfect stability and instability. In the real world, this is what really applies to most op amps. Let’s look at the behavior of an amplifier where you can’t ignore the presence of a second stage of roll-off.
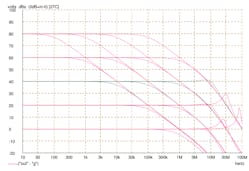
Figure 2 shows the same set of conditions as Figure 1, but this time, there’s another stage of roll-off—we’ll call it a pole—whose frequency has been fixed at 10 MHz. This graph is much more complex. It’s clear that the behavior of the “slow” amplifier, whose traces are on the left of the graph, is not significantly affected by this extra roll-off. The corresponding traces in Figures 1 and 2 are very similar. However, the more we try to push up the overall bandwidth, the more our overall result is affected by the presence of the extra stage of roll-off.
2. Shown are the same amplifiers as in Figure 1, but with an additional stage of roll-off at 10 MHz.
At high closed-loop gains, the performance is unaffected except for a faster roll-off above 10 MHz. But look what happens as we reduce the closed-loop gain. The apparent bandwidth of the circuit appears to increase, and at sufficiently low gains, there’s even a peak in the frequency response before it falls off.
This peak-then-fall behavior should set off sirens of recognition in the analog engineer—it looks like the response of a second-order lowpass filter as the “Q” factor is progressively increased. That’s exactly what is happening, and the second section of the inset box shows the mathematical derivation of the equivalent second-order transfer function for this amplifier.
The low gain curves for the fastest amplifier show clear indications of oscillatory behavior, and show why, if other stages are contributing their own roll-off, we can’t just make a faster op amp by pushing up the pole frequency of the dominating stage. However, it’s interesting to note that when our extra pole has a moderate amount of influence, it can actually flatten and extend the closed-loop frequency response beyond what the “ideal” amplifier was able to offer. Sure enough, this is taken advantage of in the design of higher-frequency op amps to provide a wider frequency range.
In the presence of some undesirable extra roll-offs, represented by the extra pole at 10 MHz we used in Figure 2, we can produce a nice op amp that won’t let you down at any closed-loop gain setting by forcing the unity-gain crossover frequency to a much lower value. But here’s an analogy to illustrate what we’re actually doing. It’s as if we built an 800 BHP Formula l race car, and then strapped on a three-ton weight to ensure that the dynamics can be simply and easily predicted with O-level [note for U.S. readers—this would be about 11th Grade] Applied Maths, without the myriad influences of all the structural and aerodynamic elements. It may be easily predictable, but boy, is it slow!
Get to the Point: What About “Minimum Stable Gain”?
All these rather theoretically derived circuits seem to be stable in simulation, just not terribly usable if the second pole is too low in frequency. Well, if you pick a criterion for the closed-loop frequency response to delineate the limit of “stability,” you can define the “minimum stable gain” to be the gain below which the criterion is violated and the response becomes “too” peaky to be useful.
Another way in which you might get into trouble when passing below that gain concerns the real-world behavior of the op amp. It might be determined not just by a second pole, but by multiple extra poles and time delays, and it may start to deviate from even this quite complicated analysis.
What is this criterion for the typical “minimum stable gain of XX” op amp? There’s no uniform industry agreement on this, which might explain why it has never been easy to explain how to use these “under-compensated” amplifiers.
For op amps intended for applications at “low” frequencies—perhaps up to the edge of the audio band—the criterion has usually been loosely phrased as “the gain that gives the same sort of transfer function that the unity-gain stable version offers at unity gain.” This explanation can be comfortable for the engineer, but did anybody spot the circular argument? Right! We need to be able to define this criterion even if the minimum stable gain is unity. In other words, it’s the kind of op amp which you can use with any amount of feedback (we’ll gloss over cases where you actually put gain in the feedback path).
Here’s a more practical definition: The minimum stable gain is the closed-loop gain that, under specified external conditions (supply voltage, temperature and particularly load impedance), causes the apparent “Q” factor of the closed-loop circuit to exceed a certain value. Often that “Q” factor value is set at 0.707, which gives the overall closed-loop response a Butterworth or “maximally flat” shape. Being quite conservative types, op-amp designers tend to build in a good deal of safety margin into this, meaning that at this gain, the ”Q” factor might indeed be a bit lower (which means “more” stable, less ringing on transients).
Why Bother to Use Amplifiers Like This?
Now that you’ve emerged unscathed from the graphs and the equations, you’ll be wanting some payback. Why do you and your engineering colleagues need to know about this, and how can you use it to your advantage?
Here’s the typical scenario. You’ve designed a circuit in which an op amp is used at a closed-loop gain of x5. The performance (possibly the distortion, which is critically affected by how much loop gain is available to suppress distortion components) at frequencies toward the upper limit of the band you’re interested in is not really good enough, and you decide that another op amp choice is needed. You find another device that offers extra bandwidth, but “hey!” who ordered all that extra supply current?
Getting four times the bandwidth from a replacement device type of similar topology probably means burning four times the power, and that might not be feasible.
Fortunately, if your vendor offers a good range of amplifiers that have had some of the compensation “lifted off”—remember that frightening word “decompensation” from the first section?—you’re saved. If you’re operating at a gain of x5, choose a device that’s optimized for at least such gains. The improvement in performance will be substantial; it takes no extra supply current and typically costs no extra money!
Some amplifier process technologies are less suited to producing “fast” amplifiers, but they may have other significant advantages such as very low wafer cost, very high supply voltage capability, ESD robustness, or particularly good noise performance. Again, in higher gain applications, an amplifier from an alternative process might be available at the right power consumption, but it might fail to meet these other needs.
…And Fast Forward to 2019
These days, in integrated analog-rich devices like Cypress’s PSoC range, the amplifiers include programmable compensation that’s typically set in system firmware to over-deliver on stability. In many applications, you can safely “reach in” and adjust the registers that set the compensation components to achieve a better gain-bandwidth product for your system.
The critical takeaway, now as then, is that “instability” isn’t a silent monster waiting to pounce if you make one tiny misstep in the use of your amplifier. Long before an op-amp circuit becomes truly unstable, it just becomes rather excitable. And let’s face it, we designers can all relate to that!