Solar power meets LEDs

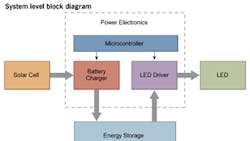
In most electronic circuits, the expected loads drive the component sizing. The situation is more complicated in the case where an alternative energy generator is the source of power. For the purposes of an example, consider a portable lantern for general illumination that must provide three hours of continuous light. This application could typically utilize 10, 20-mA LEDs. A real product design effort might calculate the light needed at a specified distance away from the lantern. That discussion would require knowledge of the optics design. The topic is important, but it is specific to the application and outside the scope of this energy-balance analysis.

Given the number and type of LEDs, a designer must decide whether to arrange them in series, parallel, or in some combination thereof. LEDs are current-controlled devices. In a series configuration, all diodes will see the same current. Thus, all LED currents will be balanced. The tradeoff is that the string voltage rises for LEDs in series, as the string voltage is equal to the number of LEDs times their forward-voltage drop. The string voltage, VLED_STRING, in this case is relatively low, just 32 V. So the series configuration has simplicity going for it, as indicated by:

V_{LED_STRING} = N х V_F-DIODE = 10 х 3.2 V ~ 32 V

Where N is the number of LEDs. Summarizing, the power converter for this case must take the input voltage, which is as yet unknown, and convert it to 32 V while providing a drive current of around 20 mA and producing an output power P of about 640 mW:

P = V_{LED_STRING} х I_{LED_CURRENT} = 32 V х 20 mA = 640 mW

Energy storage sizing

With the LED power requirements understood, we can move on to the energy storage requirements. The battery pack must provide 640 mW of power for our three-hour design target, or 1,920 mW-hrs. If the power requirement is P_LED and T is the required illumination time,

P_LED = (N х V_F-DIODE) х I_{LED_CURRENT} х T

= (3.2 V х 10) х 20 mA х 3 hrs
= 1,920 mW-hrs

Unfortunately, there are conversion inefficiencies between the battery and LEDs, including power-conversion and battery-discharge inefficiencies. These depend on a variety of factors and can vary widely. We will assume 85% and 66% for the power-converter and NiMH battery-discharge efficiencies, respectively.

Further, we may not want to let the battery run to 0% state-of-charge (SOC), as the lower the battery SOC, the shorter the battery life. For this analysis we will assume just 70% usable capacity (or 30% SOC). This means that, while the load requires 1,920 mW-hrs of energy, the usable storage device should be sized to 3,422 mW-hrs, with a total battery capacity E_B of around 4,889 mW-hrs. Using NiMH batteries, which offer a typical voltage of 1.2 V, we need approximately 4,074 mA-hrs:

E_B = P_LED/((E_PC × E_BD)×(1-SOC))

= (1,920 mW-hrs)/((0.85 × 0.66) = 3,422 mW-hrs = (3,422 mW-hrs)/(1-0.30) = 4,889 mW-hrs

where E_B = battery energy storage, mW-hrs; P_LED = LED energy requirement, mW-hrs; E_PC = power converter efficiency, %; E_BD = battery discharge efficiency, %_. However, there is an additional voltage constraint, as the minimum battery bus voltage must exceed 5 V to power the microcontroller and analog components. We can place five 1,000 mW-hr AAA batteries in series, to both maintain a > 5-V bus, as well as support the 4,074 mA-hr energy requirement.

Before continuing, it is worth asking, “What happens after the three hours elapse?” The three-hour requirement is only a design target. It is likely that, without system intervention, a user will operate the lamp as-needed, irrespective of battery-life considerations. If the battery is allowed to drain completely, it no longer makes sense to consider the SOC. Instead, assume the total energy is just the combination of the LED load plus power-converter and battery-discharge efficiencies.

However, this scenario reveals a key advantage of a microcontroller-based power supply: It gives the design team a great deal of flexibility in implementing algorithms that can do anything from mandating a hard shutoff at a particular SOC threshold to protecting the health of the battery, to allowing ride-through for emergencies. Keep in mind that, in addition to the performance numbers, there are application-usage needs and patterns that designers must consider and understand.

Solar panel sizing

Knowing the energy-storage capacity, we can size the solar cells. The 3,422 mW-hrs drawn from the battery to power the LEDs now must come from captured solar energy. Unfortunately, power-conversion efficiencies are again a factor, as is the battery-charging efficiency. For simplicity, we will use the same values as before — 85% for power-conversion and 66% for battery-discharge efficiencies. Thus the solar panel must supply 4,026 mW-hrs. Assuming six hours of charge time, the solar array must produce an average power of 671 mW.

This example has thus far dealt with straightforward energy-balance equations. There is additional complexity with regard to the needs of the photovoltaic (PV) solar cells. There are many different types of solar cells with each offering different efficiencies. Further, the amount of solar energy available depends on both geographic location and time of the year. The key concept here is solar insolation (or average irradiance), the average amount of solar energy a given surface receives. It is commonly expressed in watts per square meter.

For reference, a point on the equator (at sea level at 25°C) can expect to receive a peak solar insolation of around 1 kW/m², and the average world radiation is 250 W/m² over the course of a day. If we knew where and when (time of year) this lantern will charge, we could better predict solar irradiance. However, this is a portable application and could be used anywhere, so the world’s average daily irradiance of 250 W/m² is a good place to start.

With an expectation of average solar insolation, we can calculate the electrical energy the solar energy will generate. While solar cell efficiencies range from 6 to over 40% (in the lab), 10 to 15% efficient solar technology is common, available, and reasonably economical. So a ballpark figure is that 15% of the 250 W/m² gets converted into usable electrical power. The requirement for 4,026 mW-hr of energy and six hours of charge time reveals a need for a solar panel 179 cm² in size.

E_B = (I_rrAVG × E_sc) × A × T_c

Solving for A,

A = 4,026 mW-hrs/((250 W⁄m² × 0.15) × 6 hrs)

= 179 cm², or 5.5 in²

where I_rrAVG = average solar cell current, A; E_sc = solar cell efficiency, %; A = solar cell area, cm²; and T_c = charging time, sec.

While the example provides some specific numbers, it is useful to review how each component influences the overall system performance. The nearby table shows some of the key factors that influence the duration over which the system can generate LED light, as well as how long it takes to recover that energy.

The data contain no surprises, but do prompt some observations. Incandescent bulb technology has an efficacy of approximately 14 to 16 lm/W. It’s clear that an 850 lm/W (~65-W bulb) requirement from a 15 lm/W light source requires an unreasonable amount of energy storage. For reference, a standard D-Cell battery offers about 10,000 mA-hrs. (That’s three D-cells for 30 min, or 18 D-cell batteries, to provide three hours of lighting). The rest of the figures deliver a similar message, and demonstrate the tradeoffs of light output, solar-cell efficiency, and solar-panel size.

The application needs drive the sizing of core components, which in turn determine powertrain components for both the battery-charging side (solar to battery) as well as the LED driver stage (battery to LEDs). A microcontroller-based implementation can take full advantage of the latest LED, solar and battery technologies, and maintains the flexibility to respond to their respective technology development trajectories.

For instance, Li-ion batteries offer charge/discharge efficiencies approaching 97%, compared with NiMH 66% charge/discharge efficiency. This affects the size of the energy storage as well as its electrical qualities, the charging profile, and the required size of the solar panel. A microcontroller-based design can quickly and easily be modified to take advantage of this technology, with minimal impact on the rest of the architecture and components.