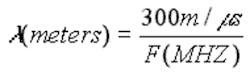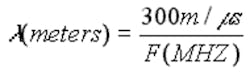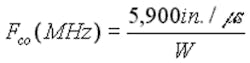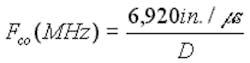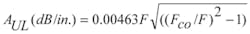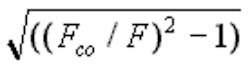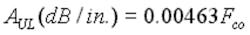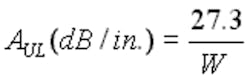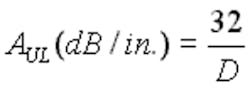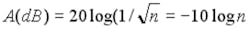The best possible shielding is provided by a solid metal enclosure with no seams, no penetrations, and no apertures. The shielding can’t get any better than that—absolutely no RF leakage.
But of course, a solid enclosure is useless. Shielding material doesn’t have to be very thick to be an outstanding shield, especially at high frequencies. However, even though we need them, one little hole in the shield can change all that—and the bigger the hole, the bigger the leak.
So when is a hole not a hole? When an integrally attached metallic tube changes it into a waveguide.
A waveguide is a high-frequency transmission line. Everyone is familiar with transmission lines, although we may not call them by that name. For example, the 50- or 60-Hz power lines that deliver power to our homes and businesses and then across the country are power frequency transmission lines. The twin-lead or coaxial cable that runs from the antenna to the television set is an RF transmission line.
The purpose of these two-conductor transmission lines is to guide power, radio, TV, and other electrical signals from one place to another with a minimum loss of energy. The signal voltage in one lead induces current in its closely coupled return lead, and a wave propagates down the transmission line.
The Waveguide
Signal frequency is inversely related to its wavelength, as expressed by the following equation:
As the frequency increases, its wavelength gets smaller. Once the signal frequency increases to the point where its half-wavelength (l/2) is smaller than the spacing between the transmission-line conductors, a new propagation mode can exist, and the conductors can be configured as a hollow tube or waveguide. At these frequencies and higher, the RF energy can propagate through a hollow tube, essentially a single-conductor transmission line.
Although there are several popular waveguide configurations, the rectangular cross-section is the easiest to visualize. In this case, the waveguide’s cutoff frequency ( Fco ) is determined by its width, which must be slightly wider than l/2.
The height is independent of frequency, but a 2:1 width-to-height ratio is very popular. At this ratio, the RF energy entering the waveguide reflects at an angle from side to side and travels through the tube with very little loss.
A waveguide is very efficient at passing all frequencies above its Fco, acting like a high-pass filter. For example, at 10-GHz, transmission-line losses in a 2-in. rectangular copper waveguide range from approximately 0.02 to 0.12 dB per meter length, depending on height.
There are a number of possible RF transmission modes, but from a shielding perspective, it is the waveguide’s behavior below cutoff for its lowest frequency propagation mode, such as the TE10 mode, that is of interest. Below its Fco, a waveguide is not a good transmission line, and it has very high attenuation.
Waveguide Attenuation
Energy is not dissipated in the waveguide; it is reflected back to its source. Consequently, using a waveguide below cutoff provides a way to have a hole in a shielded enclosure and still maintain high levels of attenuation—at least for frequencies below its Fco. The lowest Fco (TE10 Mode) for a rectangular and a circular waveguide is given by the following equations:
Rectangular:
Circular:
where: W = width in inches
D = diameter in inches
Below the Fco, the attenuation per unit length (inches) at any frequency (F) is given by:
where: AUL = attenuation per unit length
Although this equation provides the attenuation per unit length, the designer using these relationships should always strive for at least a 3:1 length-to-width (L/W) or diameter ratio. Figure 1 shows a plot of this equation for several sizes of rectangular waveguides with width dimensions from 0.1 to 2 in. with a 5:1 L/W ratio. Regardless of the width, for frequencies below approximately Fco/3, the attenuation is almost independent of frequency. When the frequencies are below Fco/10, the quantity
approaches (Fco/F), and we can approximate the attenuation per unit length by:
After substituting the appropriate Fco for the rectangular and circular waveguide, the attenuation per unit length reduces to:
Rectangular:
Circular:
where: W = width in inches
D = diameter in inches
Figure 2 shows a plot of these two equations along with plots of their respective Fco. These plots provide the attenuation per inch of length for a rectangular or a circular waveguide with width and diameter dimensions ranging from approximately 0.1 to 1.4 in. for RF energy that enters the waveguide. The Fco scale shows the upper frequency limits where the waveguide dimensions no longer provide the corresponding attenuation values.
Not all of the RF energy that is incident on an open waveguide actually is transmitted into the opening. Some of it reflects from the opening. In addition, not all of the energy that actually enters the waveguide will excite propagating waves within the waveguide.
It is very difficult to analyze these separate characteristics, but remember that Murphy’s Law prevails. In any case, using a hole configured as a waveguide below its Fco permits us to create openings with very high attenuation. For example, a 0.25-in. hole drilled in a 1-in. thick aluminum plate has an Fco of 6,920/0.25 = 27.7 GHz. With its 4:1 depth-to-diameter ratio, it will provide more than 120-dB attenuation (A = 32 × 4) to approximately 9 to 10 GHz and outperform the same size aperture (in thin materials) over the entire frequency range.
This only is true as long as there are no conductors introduced into the hole. Put a center conductor through a tube and the configuration no longer is a waveguide; it’s a coaxial cable.
Even though waveguide penetrations can’t be used as entry points for conductors like wires and pipes that penetrate a shield, they still are very important. They are used anywhere the transmission of light, sound, gases, and nonconductive fluids; the entry of nonconductive materials such as drive shafts or belts; or the movement of small-sized objects (which may be conductive) through the walls of a shielded enclosure is required while maintaining high levels of attenuation.
Table 1 (below) lists a number of examples of waveguide penetrations. Most of these applications are single waveguides, and the equations can be used to determine their overall attenuation. As long as their separation at problem frequencies is greater than l/2, multiple waveguides will act independently. However, when they are closely coupled, such as closer than l/2, they do not act independently, and the number of closely coupled apertures (n) reduces the maximum attenuation by:
Honeycomb ventilation panels are good examples of closely coupled waveguides and can be used to better explain the significance of this equation. Typical honeycomb panels 0.5-in. thick are made up of 0.125-in. diameter hexagonal tubes that share a common wall.
Table 1. Examples of Waveguide Penetrations
(low frequencies only)
The configuration creates closely coupled waveguides with a 4:1 length-to-diameter ratio. If they were perfect, each cell would occupy an area of 0.1227 in.2 on the panel face and provide more than 120-dB attenuation. A panel 20 in. × 20 in. with an area of 400 in.2 would have 3,260 cells.
The decrease in attenuation for this panel would be A(dB) = -10 log 3,260 = 35 dB, resulting in an overall panel attenuation of approximately 90 dB. The reduction in attenuation generally is not that bad, especially for near fields at the higher frequencies. This is due to varying wave-front entry angles along with exiting fields from holes spaced apart by more than l/2 not recombining in phase. Paradoxically, this implies that as the frequencies increase there would be fewer holes within the l/2 separation criteria, so the shielding would increase.
However, this is not the case. As wavelengths become smaller, waveguides can support more and different propagation modes and greater coupled energy can enter the waveguides. Still, honeycomb vent panels can be constructed to provide more than 120 dB at 18 GHz without significant airflow restrictions.
References
Kraus, J.D., Electromagnetics, McGraw Hill, 1953.
Kodali, V.P., Engineering Electromagnetic Compatibility, IEEE, 1996.
Ramo, S. and Whinnery, J.R., Fields and Waves in Modern Radio, John Wiley, 1944.
Smith, B.L. and Carpentier, M.H., The Microwave Engineering Handbook, Volume 1, Chapman & Hall, 1993.
About the Authors
Ron Brewer is vice president of EMC technical services at Instrument Specialties. He is a NARTE-certified EMC/ESD engineer with more than 25 years in EMC/ESD/Tempest engineering. Mr. Brewer serves on three technical committees and, as an internationally recognized EMC authority, has made more than 185 technical presentations in North America, Europe, Asia, and the Pacific. He also has been named a Distinguished Lecturer by the IEEE EMC Society. Instrument Specialties, P.O. Box 650, Delaware Gap, PA 18327, 570-424-8510.
Published by EE-Evaluation Engineering
All contents © 2001 Nelson Publishing Inc.
No reprint, distribution, or reuse in any medium is permitted
without the express written consent of the publisher.
January 2001