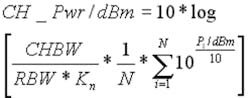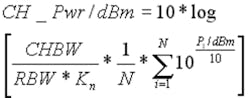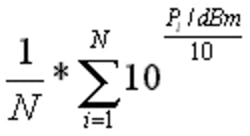Today’s emphasis on connectivity enables you to control your spectrum analyzer from the other side of the world. That makes it doubly important to understand how different settings and signal conditions can affect the information displayed.
For example, a typical global system for mobile communications (GSM) measurement is shown in Figure 1. Important control settings and measurement results are clearly presented. As shown, the IFR Model 2399 Spectrum Analyzer uses sets of colored cursors to highlight measurement areas; in this case, the center 50 kHz of the occupied channel and upper and lower adjacent channels.
What is being measured? The horizontal center of the display is set at 900 MHz, and the total span is 1 MHz or 100 kHz per division. The top line of the graticule corresponds to 0 dBm, each vertical division represents 10 dB, and the signal has been attenuated by 10 dB. The measurements and displayed levels take into account the attenuation.
GSM transmits in two 25-MHz bands: 890 to 915 MHz from the mobile transmitter to the base station and 935 to 960 MHz from the base station to the mobile receiver. The bands are divided into 200-kHz channels, and the 50th mobile transmit channel, centered on 900 MHz, is shown in Figure 1. The displayed signal clearly is an unmodulated carrier because of its narrow bandwidth. In actual operation, a GSM burst occupies slightly more than the 200-kHz channel bandwidth.
According to the GSM standard, a time slot during which a single channel burst is transmitted lasts 0.58 ms. Slow hopping, a reassignment of frequencies, is at a rate of 217 frequency changes/s. These two facts, together with the sweep time of 1.3 s, allow you to infer that this is a static test without time- or frequency-hopping. There is nothing to indicate that the 900-MHz signal is intermittent.
To ensure good definition, a resolution bandwidth (RBW) filter of 1 kHz has been selected. Analog filters in newer spectrum analyzers have a 3-db:60-dB shape factor of about 11. This means that the bandwidth of the filter 60 dB down from its peak response is 11 times as wide as its response 3 dB down, in this case, 11 kHz vs. 1 kHz.
In contrast, digital filters typically achieve shape factors of less than five. For this example, the effect is as though a bandpass filter with a 50-kHz, 3-dB bandwidth were used but only 60 kHz wide, 60 dB down. That’s almost a rectangular passband and ensures that little power from outside the 50-kHz area is included in the average power calculation. As a comparison, if RBW equals 50 kHz, and the filter is analog rather than digital, the width 60 dB down equals 550 kHz.
The 4.97-dBm value is the signal level at marker 1. It’s not totally obvious from the figure, but to bring the noise floor onto the screen, the trace has been offset upward by 10 dB. This is the reason that the peak reading is higher than the reference level: the peak has been deliberately positioned off the top of the graticule.
If that’s the case, then why doesn’t the Main channel power (CHP) reading of 7.55 dBm agree with the peak marker 1 value of 4.97 dBm? The reason is that Main CHP is computed across the 50-kHz measurement bandwidth, but the marker 1 value corresponds to the peak. Equation 1 defines the integrated bandwidth method of making this calculation.
where: CH_Pwr = channel power
CHBW = channel bandwidth
Kn = ratio of noise bandwidth to RBW
N = number of pixels within the channel
Pi = level in decibels referred to 1 mW (dBm) represented by the ith trace pixel
In Figure 1, RBW equals 1 kHz and CHBW equals 50 kHz. The power levels associated with each pixel between the red cursors are converted from logarithmic dBm to linear milliwatts and averaged. Then the power level is adjusted upward to account for the ratio of the measurement bandwidth to the RBW.
For a spectrum analyzer with a VGA display, 500 pixels often correspond to the size of the 10-division horizontal graticule. On this basis, there are 25 pixels between the red cursors, each pixel corresponding to 2 kHz. The second half of the equation
simply is the average of the linear power levels within the 50-kHz measurement bandwidth. If you assume that the 900-MHz peak is only one pixel wide, then the average is the 3.14-mW peak divided by 25, the number of pixels, equals 0.126 mW.
The ratio of noise power bandwidth to RBW is 1.06 for four- or five-pole Agilent Technologies filters with Gaussian response, so Kn equals 1.06. Assuming that IFR RBW filters behave in a similar way to Agilent RBW filters, the first term becomes 50/1.06 = 47.2. The overall result is 7.73 dBm.
That’s close to 7.55, but how can the power just calculated be greater than the displayed power when the peak has been assumed to be only one pixel wide? Well, the peak probably is less than 2-kHz wide—the width of one pixel. Some spectrum analyzers subdivide pixels to get greater measurement resolution. In this case, it’s easy to see that the width of the continuous wave (CW) tone could be less than the 2 kHz represented by a single pixel, for example, 1.8 kHz.
If each pixel were subdivided into 10 parts, the average power would be 3.14 × 1.8/2/25 = 0.113 mW. The Main CHP now equals 7.27 dBm. Of course, there is some power contributed from the rest of the 50-kHz measurement bandwidth, but the single-pixel-wide peak extends for about 25 dB. This means that power from areas where the displayed signal is two or more pixels wide is more than 300 times less than the peak power, so it doesn’t add very much to the total.
The display of a very narrow CW tone and relevant measurements is problematic in a digital system. By definition, a line cannot be less than one pixel in width. On the other hand, the actual signal may well be very narrow.
The last variable displayed, the video bandwidth (VBW), has been set to 1 kHz. In contrast to the RBW that determines the amount of the signal’s energy to reach the detector, the VBW deals with display of detected levels. If the RBW is large, more noise will reach the detector. Selecting a VBW that is narrow compared to the RBW will smooth the display and requires increased sweep time. For some signals, the combination of fast sweep, wide RBW, and narrow VBW is optimal.
A VBW that is small compared to the RBW means that the displayed spectrum cannot follow detected fast peaks so they will become distorted. A noticeable but not severe reduction in noise occurs for VBW equals RBW. In Figure 1, the intention has been to reduce the size of the noise floor somewhat because it wasn’t important to the measurement being made.
It’s Harder Around the Edges
Even the best spectrum analyzers are not perfect. The sources of error include signal compression if the input mixer level is too large, internally generated thermal noise, internal oscillator phase noise, second harmonic distortion, and third- and fifth-order distortion.
For example, if two signals of equal power but at frequencies f1 and f2 drive a perfectly linear amplifier, the output will contain only the two original frequencies. The nonlinearities present in a real-world amplifier result in many combinations of the two frequencies, including but not limited to 2f1-f2, 2f2-f1, 3f1-2f2, 3f2-2f1…
A spectrum analyzer behaves like a weakly nonlinear amplifier, and its response can be represented by a power series, Vo=a1Vi+a2Vi2+a3Vi3+…+anVin, where rms voltages are assumed, and Vi corresponds to the power at the input mixer and Vo to the detected power.
This means that in addition to a simple gain term, a1, there will be higher order terms generated. The third- and fifth-order intermodulation distortion (IMD) terms are particularly important when attempting to maximize the spectrum analyzer’s dynamic range.
For relatively simple tests, modern spectrum analyzers couple the various control settings that can affect measurement accuracy. For example, the Auto Couple mode in the Agilent Model E4440A links RBW filter, VBW filter (VBW equals RBW is the default), span, and sweep time. The reference level tracks the input attenuator setting.
The suggested measurement procedures given in Reference 1 ensure that the IMD products generated by the spectrum analyzer are at least 18 dB below those of the DUT itself. This means that the distortion caused by the spectrum analyzer will affect the measurement of DUT distortion by less than 1 dB.
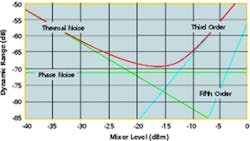
However, more difficult measurements such as the adjacent channel power ratio (ACPR) or low-level IMD require a deeper look at your spectrum analyzer’s capabilities. Figure 2 shows the relationships among a spectrum analyzer’s thermal noise, phase noise, and third- and fifth-order distortion as functions of the mixer level. It’s complicated because the dynamic range required for accurate ACPR measurement stretches the performance of many spectrum analyzers to the limit. This is the reason that you need to consider so many things before you can be confident that your measurements are sound.
Figure 2. Dynamic Range Chart for cdmaOne at 885-kHz Offset
CDMA: One Channel, Many Conversations
Figure 3 (see the June 2001 issue of Evaluation Engineering) shows a number of power measurements being made on an IS-95 code division multiple access (CDMA) transmission. CDMA signals resemble noise. This is important because noise-like signals ideally limit the choice of display detector to averaging or rms types. Positive or negative peak-reading detectors bias the value of each pixel in the measurement range. Sample detectors merely accept the last value of the set of amplitudes corresponding to the frequency span represented by a pixel.
Averaging and rms detectors operate independently of the signal statistics. They give the most repeatable results. On the other hand, because average power results from averaging the power levels of all the pixels in the measurement range, a sample detector can be used if there are enough pixels; 1,000 are required for a measurement repeatability of 0.1 dB.1
Averaging the range of pixel values produced by either a sample or an averaging detector is not straightforward. Unfortunately, the average of the logarithms of quantities A, B, and C isn’t equal to the log of the average of those quantities. rms detectors have become popular because they provide linear values that can be averaged in a straightforward manner.
It also may be important to avoid small values of VBW. “May” has been used because in some architectures, such as the Agilent PSA E4440A, the VBW setting doesn’t affect rms power average measurements, just the displayed trace. A small VBW means that the displayed spectrum can’t correctly follow peaks. If true random noise is being filtered, using a small VBW gives predictable and desirable smoothed displays. CDMA signals resemble noise, but their statistical makeup is different, so CDMA signals shouldn’t be smoothed by using a small VBW.
Video averaging averages successive displayed spectra and is another way to reduce noise. Unfortunately, displayed spectra usually are scaled logarithmically, and we’re back to the argument about averaging logs.
For Figure 3, RBW equals 30 kHz, CHBW equals 1.23 MHz, and Kn is again assumed to be 1.06. Because of the stringent specifications on ACPR, an RBW filter with 1% to 4% of the channel bandwidth is selected to provide a very sharp falloff at each edge of the channel: 30 kHz/1.23 MHz = 2.4%.
Because the modulated signal power is spread across the entire measurement bandwidth, transmitting-channel power is calculated according to Equation 1. You can think of similar amounts of power existing in each of a series of 30-kHz RBW frequency bands between the C0 cursors.
CDMA is a broadband technology, and all the power in all the bands exists simultaneously. Consequently, the ratio of CHBW/RBW is more obviously the correct scaling factor than it may have seemed to be when applied to the narrowband signal in Figure 1.
If CHBW equals 1.23 MHz and RBW equals 30 kHz, then the value of the first fraction inside the brackets is 38.7. The second half of the equation is the average displayed power level. This is estimated to be about -18 dBm or 0.0158 mW, just averaging the top of the pulse by eye.
Multiplying by 38.7 and converting to dBm yield -2.12 dBm. That’s close enough to the -1.65 dBm reported as Tx Channel Power to prove the concept. As a check, assume the average power had been -17 dBm. This value corresponds to -1.12 dBm, so -18 dBm was a good guess.
The cursors and control values displayed in Figure 3 automatically are set up when the Rohde & Schwarz Model FSU Spectrum-Analyzer user selects an ACPR measurement. For example, the measurement bandwidth of the adjacent and first alternate channels is only 30 kHz, not the 1.23 MHz of the transmitting and second alternate channels. The 885-kHz spacing from the center of the transmitting channel to the edge of the adjacent channels is equal to a 270-kHz guardband plus half of the 1.23-MHz transmitting channel width.
Generally, a number of CDMA phones operate simultaneously. This means that peaks will appear in the base station transmitted spectrum caused by the random addition of separate customer’s encoded signals. The result is a peak-to-average ratio that can be as large as 12 or 14 dB. The peaks may drive the mixer into compression even if the average power is well inside the linear region.
Also, because so many frequencies are present within a CDMA signal, third- and fifth-order distortion become important considerations. Finally, phase noise must be considered. It’s a limiting factor for IS-95 CDMA, but much less important for wideband CDMA (W-CDMA) given the larger offsets specified for the ACPR measurement.
Summary
When choosing a spectrum analyzer, determine what types of measurements the different models support. For example, zero-span operation with special time-domain measurement routines is useful for GSM and time division multiple access (TDMA) testing. Appropriate features include time gating and a combined rising/falling edge burst measurement mode.
Spectrum analyzers are complex instruments. To ensure spectral purity, several IF stages are used, each contributing to the overall inaccuracy, nonlinearity, and noise. One way to partially avoid these problems is to use a spectrum analyzer that acquires wideband data in real time and computes the spectrum by using the FFT. Generally, FFT-based spectrum analyzers have a shorter signal path and may offer a larger dynamic range than many swept-filter spectrum analyzers.
There are time-domain methods available for ACPR measurement, for example, that yield much faster results than a swept spectrum analyzer. Reference 2 describes an approach claimed to yield a 20× speed improvement. It is also said to allow measurement of switching transient effects within the channel, something not possible with swept spectrum analyzers.
But, without taking a different approach, you have to believe your spectrum-analyzer measurements. Obtaining the best accuracy only can be done by thoroughly understanding the effect of signal type and level and control settings. Several sources listed as additional information below address aspects of spectrum-analyzer measurement problems and suggest appropriate techniques.
References
- Optimizing Dynamic Range for Distortion Measurements, Agilent Technologies Product Note 5980-3079EN, November 2000.
- Wolf, J., “A New Method for Fast ACP Measurement With Spectrum Analyzers,” Proceedings of the Wireless and Portable by Design Symposium, Spring 2000.
Additional Information
- Spectrum Analyzer Basics, Agilent Technologies Application Note 150, 5952-0292, November 2000.
- Zarlingo, B. and Gorin, J., “Spectrum Analyzer Detectors and Averaging for Wireless Measurements,” Proceedings of the Wireless and Portable by Design Symposium, Spring 2001.
- Avenell, B. and Jordan, I., “Optimizing Dynamic Range for Wireless Measurements,” Proceedings of the Wireless and Portable by Design Symposium, Spring 2001.
- Wolf, J. and Tiepermann, K., “Measuring ACPR of W-CDMA Signals With a Spectrum Analyzer,” Proceedings of the Wireless and Portable by Design Symposium, Spring 1999.
Return to EE Home Page
Published by EE-Evaluation Engineering
All contents © 2001 Nelson Publishing Inc.
No reprint, distribution, or reuse in any medium is permitted
without the express written consent of the publisher.
June 2001