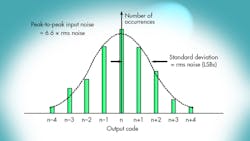
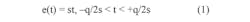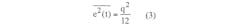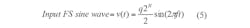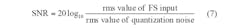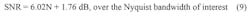The maximum error made by an ideal converter when digitizing a signal is ±½ LSB, as shown in the transfer function of an ideal N-bit ADC. The quantization error for any ac signal that spans more than a few LSBs can be approximated by an uncorrelated sawtooth waveform having a peak-to-peak amplitude of q, the weight of an LSB. Another way to view this approximation is that the actual quantization error is equally probable to occur at any point within the range ±½ q.
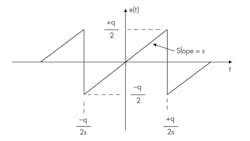
The quantization error as a function of time is shown in more detail in the figure. A simple sawtooth waveform provides a sufficiently accurate model for analysis. The equation of the sawtooth error is given by:
The mean-square value of e(t) can be written as:
Performing the simple integration and simplifying:
The root-mean-square quantization error , therefore, is:
The sawtooth error waveform produces harmonics that extend well past the Nyquist bandwidth or dc to Fs/2, where Fs = converter sample rate. However, all these harmonics fold (alias) back into the Nyquist bandwidth and sum together to produce an rms noise equal to q/√12.
Quantization noise is approximately Gaussian and spreads uniformly over the Nyquist bandwidth of interest, typically dc to Fs/2. The underlying assumption here is that the quantization noise is uncorrelated to the input signal. The theoretical signal-to-noise ratio can now be calculated assuming a full-scale input sine wave:
The rms value of the input signal, therefore, is:
Therefore, the rms signal-to-noise ratio for an ideal N-bit converter is:
