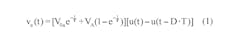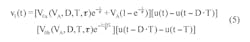Accurately Determine Steady-State Output For A Periodically Driven RC Filter

This analytical and graphical technique allows engineers to determine, in closed form, the output of an RC filter driven by a PWM pulse train. It is based on the principle that current and voltage cannot change instantaneously in a real-world circuit, and the endpoint of one time phase or state of a circuit is the beginning point for the next phase.

Keng Wu

Nov. 15, 2013

3 min read

655533676d70a4001e8e69a7 Ifd Electrical Engineer Scanrail Dreamstime

This article is part of the Ideas for Design Series: Vol. 3, No. 9.

A recent Idea for Design showed a graphical technique for determining the output of an RC filter driven by a pulse-width modulation (PWM) pulse train.¹ It requires the manipulation of infinite series with a limit. Therefore, it does not yield steady-state results with confidence.

Related Articles

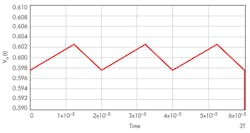
A better approach uses the concept of continuity of states and steady-state “wrap-around” to eliminate this shortcoming, since current and voltage values in a real circuit cannot change instantaneously. Current and voltage are variables with continuous values in time, from moment to moment. For a circuit structure that is switched periodically among several states repeatedly, the end state of one structure serves as the starting state of the next.

Using the same RC filter, periodic-input pulse train, and designations as the referenced Idea for Design, Equation 1 shows the filter output when the driving source V_A is non-zero:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 1

When the driving source drops to zero, the output is given by:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 2

In Equation 1 and Equation 2, the two starting conditions V_0a and V_0b are yet to be determined. A gating function with unit steps is also used. At steady state and at the switching boundaries, t = DT and t = T, so Equations 3a and 3b must hold:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 3

This indicates that the end state of active duration with non-zero driving source must act as the starting state, V_0b, of the inactive duration with zero drive. Similarly, the end state of the inactive interval must return to the same starting state, V_0a, of the active segment. Using these facts and Equations 3a and 3b, we get:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 4

In other words, cyclic starting states are actually known functions of driving source V_A, duty cycle D, pulse period T, and time constant RC = τ. The steady state output in one cycle can be written as:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 5

where the multiple-cycle output is given by:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 6

Using the example of the previous Idea for Design, with V_A = 1, D = 0.6, T = 20 μs, and τ = 50T, produces the steady-state results of the figure. The output dc level (Equation 7) is obtained by taking the average of Equation 5:

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Eq 7

and confirms Equation 16 of the previous approach.

The approach presented here gives the true steady-state output in compact, closed form with a high degree of confidence. The technique can be extended to other second- and higher-order circuits that are switched periodically among multiple states.^{2, 3}

Electronicdesign Com Sites Electronicdesign com Files Uploads 2013 11 Ifd2567 Fig

Analysis shows that the steady-state output of this RC filter, when driven by a 50-kHz, 1-V, 60% duty-cycle PWM wave, is also periodic and stays within a narrow amplitude band.

References

1. “Graphically Determine The Output Signal Level Of An RC Filter,” Electronic Design, Oct. 3, 2013.

2. Switch-mode Power Converters, Keng Wu, Elsevier, 2005, ISBN 13:978-0-12-088795.

3. Power Rectifiers, Inverters, and Converters, Keng Wu, Lulu.com, 2008, ISBN 978-1-4357-2023-7.

Keng C. Wu has a BS from Chiaotung University, Taiwan, and an MS from Northwestern University, Evanston, Ill. He has published four books and holds seven U.S. patents. He can be reached at [email protected].

About the Author

Keng Wu

Keng C. Wu, a power electronics consultant, has published five books on power processing, was awarded “Author of the Year” twice (2003 and 2006 Lockheed Martin), and presented a 3-hour educational seminar IEEE APEC-2007 S17. He has held more than a dozen U.S. patents. He earned a BS from Chiaotung University, Taiwan, and an MS from Northwestern University, Evanston, Ill.