When evaluating the dynamic performance of precision analog-to-digital converters (ADCs) using fast Fourier transform (FFT) analysis, coherent sampling typically is used to accurately measure the noise and distortion spectral components in the FFT. In applications where the coherent sampling criteria cannot be met, a window weighting function is applied to minimize spectral leakage. Designers should know how to select an optimal FFT windowing function when testing the performance of precision ADCs using a single-tone signal.
This file type includes high resolution graphics and schematics when applicable.
On The Bench
The FFT analysis is a common method used to characterize an ADC’s dynamic performance. This test method typically involves applying a pure, low-noise, low-distortion sinusoidal signal at the ADC’s inputs. Samples are taken over a time interval and perform the ADC data FFT to quantify the noise and distortion spectral components in the frequency domain.
Related Articles
- Understand Signal Analysis In The Time, Frequency, And Modulation Domains
- The Fundamentals Of Spectrum Analysis
- FFT Brings Spectrum Analysis To The Scope
The FFT is an algorithm that quickly performs the discrete Fourier transform of the sampled time domain signal. The FFT requires a time domain record with a number of samples (M) that is a power of 2. The FFT spectrum consists of M/2 discrete frequency bins with a range from dc to fS/2, and a bin width of fS/M, where fS is the sampling frequency.
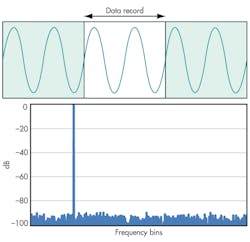
The FFT assumes the signal within the time record is repetitive (Fig. 1). If the samples on the time record do not start and stop within the same value at the end points in the time domain frame, this is interpreted as a discontinuity in the waveform.
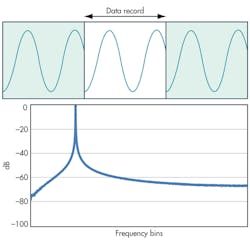
The abrupt discontinuity at the record’s end points produces frequency components not present in the original signal, which introduces spectral leakage in the FFT. This can be understood by looking into the case where the sampled signal is a sinusoid (Fig. 2).
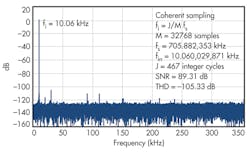
Coherent sampling ensures that an integral number of cycles of the input signal is included within the time frame. When coherent sampling is utilized, the resulting FFT displays only the frequencies corresponding to the input frequency and its harmonics. The criterion for coherent sampling is given by:1
Mfi = JfS (1)
Where M is the number of samples in the data record, fi is the frequency of the input signal, J is an integer prime number of cycles of the input waveform in the data record, and fS is the sampling frequency. To accomplish coherent sampling, the input signal frequency and/or the sampling frequency is finely adjusted to meet the relation in Equation 1. Figure 3 shows illustrates an FFT of a sinusoidal signal using coherent sampling.
To precisely meet the coherent sampling criteria, the test setup requires a function generator that allows a fine adjustment of the input signal frequency. Additionally, the function generator typically is phase-locked with the clock-signal generator used to trigger the sampling of the ADC.
Windowing
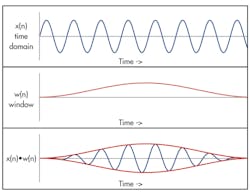
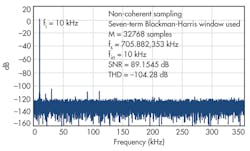
In applications where the coherent sampling criteria cannot be met, a window weighting function can be applied to the time record to minimize spectral leakage. Windowing consists of multiplying the data in the time domain by a window function (Fig. 4).
Different window functions are available with different frequency response characteristics. Choosing an optimal window for a specific application requires knowledge of the signals involved, consideration of the frequency resolution, and the dynamic range requirements (Fig. 5).
In this application, a single-tone signal is used for dynamic testing of high-resolution ADCs. The optimal window function requires a high dynamic range to accurately resolve noise and distortion components in the frequency spectrum. Consider an ideal ADC, where the signal-to-noise ratio (SNR) is given as a function of the number of bits (N):
SNRIdeal = 6.02 N + 1.76 (dB) (2)
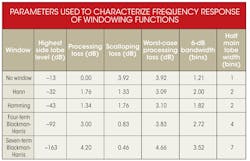
Using Equation 2, the SNR for an ideal 14-bit ADC yields 86 dB, and the SNR for a 16-bit ADC is 98 dB. The necessary side lobe attenuation level should exceed the dynamic range of the ADC under test by some margin. The table lists parameters used to characterize the frequency response of a few windowing functions.
The Hann and Hamming windows do not offer enough side lobe attenuation to be used to test high-resolution ADCs. The four-term Blackman-Harris function has a side lobe rejection level that allows us to accurately test a 12-bit ADC converter. However, this window is not adequate to resolve the SNR of a 16-bit resolution ADC. The seven-term Blackman-Harris has enough dynamic range to resolve the FFT spectral components of a 24-bit resolution ADC.
When using a single-tone sinusoidal signal, the SNR, with respect to the carrier, is calculated as the ratio of power of the tone signal (PSignal) to the power of the noise components in the spectrum (PNoise), excluding the harmonics of the signal as shown in:
SNRdB = 10log10(PSignal/PNoise) = PSignal(dB) – PNoise(dB) (3)
For example, if the seven-term Blackman-Harris window is selected, the fundamental and its harmonics will spread across the window main lobe width bins (±7 side bins around the signal). Therefore, prior to performing the SNR calculation, you need to remove these bins around the signals when calculating the noise power.
Processing loss is the reduction in SNR due to the signal spreading across the main lobe width. Because of this spreading in the signal power, a gain correction factor must be used to accurately compute SNR. The processing loss assumes the frequency of the test signal falls exactly in the middle of the frequency bin. Since the input frequency may not match exactly the frequency bin in a non-coherent test setup, the scalloping loss is the perceived signal attenuation in the FFT when the signal frequency component falls exactly between bins. The worst-case processing loss is the sum of the processing loss and scalloping loss, and it provides a measure of the maximum SNR reduction due to the window function and the worst-case frequency location.2
Conclusion
When evaluating the dynamic performance of precision ADCs using FFT analysis, coherent sampling provides the best results. In cases where coherent sampling cannot be achieved, a window function with low-side lobes is required to resolve the noise and harmonic components in the frequency spectrum. For example, when using non-coherent sampling, the SNR and THD is estimated after applying an FFT window function and the processing loss correction factor.
References
1. Dominique Dallet and Jose Machado da Silva (2005), Dynamic characterization of analogue-to-digital converters, Dordrecht, the Netherlands: Springer, Chapter 4, pp. 86-88
2. Bores Signal Processing, “FFT Window Functions: Limits on FFT Analysis,” http://www.bores.com
3. Frederick J. Harris, “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform,” Proceedings of the IEEE, vol 66, pp. 51-83, January 1978
4. For more information about ADCs, visit www.ti.com/adc-ca
5. Need a trusted source to quickly find reference designs for your system design? TI Precision Designsis a library of complete board- and system-level circuits designed to help engineers quickly evaluate and customize their systems while expanding their analog knowledge base: www.ti.com/precisiondesigns-ca.
Luis F. Chioye is an applications engineer with TI’s Precision Analog group, where he is responsible for precision data converters. He received his BS in electrical engineering from the University of Arizona, Tucson, and his MS in electrical engineering from Walden University/NTU School of Engineering and Applied Science, Minneapolis, Minn. He can be reached at [email protected].