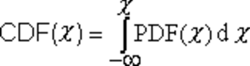Your new job assignment is to write the purchasing justification for a modern RF power meter. You already know a lot about RF applications from your amateur radio experience years ago. It shouldn’t be difficult to complete the evaluation of a few meters within the two-week time frame you’ve been given.
True to the manufacturers’ promises in their glossy brochures, the meters really are easy to use. All the functions give the kinds of results you expect, but there is a separate statistical mode you hadn’t run into in the past. Do you need a statistical mode? What is it used for? Why do only newer model meters have this mode? Suddenly, what seemed like the comparison of straightforward power meters just got much harder.
Why You Need Statistical Measurements
The RF power measurement problem has been complicated by the recent deployment of code division multiple access (CDMA) wireless communications equipment. There are other types of digitally modulated signals, but CDMA exploits spread-spectrum technology. It modulates the carrier with a pseudorandom sequence having values of +1, -1, and sometimes 0 depending on the details of the particular system.
The resulting signal looks very much like noise. In fact, CDMA signals can have a negative signal-to-noise ratio (SNR) and literally be lost in the background noise. CDMA communication only is possible because receivers use matched filters to reliably recover the signal.
Fortunately, the characteristics of random noise as it occurs in electronic systems are well understood. In most cases, noise can be treated as a random variable with a Gaussian or normal distribution. Ordinarily, you can say with certainty that the voltage at a point is 1.0 V. But when dealing with a particular signal distribution, it makes more sense to say, for example, that the randomly varying signal measures >1.0 V for 25% of the time.
A random variable is described by its probability distribution function (PDF). The normal PDF shown in Figure 1 (see June 2000 issue of EE) corresponds to Equation 1. There is the same probability of a point being n units less than the mean as being n units greater because of the squared term in the exponent. It causes the curve to be symmetrical.
where: c = the value of the random variable
s = its standard deviation
µ = its mean value.
The X axis is divided into units of s, which is a measure of dispersion, or the degree to which points are not located close to µ. Scaling the axis in this way means that the curve in Figure 1 already has been normalized to an extent. Regardless of the s associated with different sets of data, if the data sets are normally distributed their PDF curves will be similar.
In contrast to the textbook PDF, plots of PDF curves generated by a real process will appear ragged, not smooth. The distinction here involves the concept of limits that separates differential from difference equations. The textbook curve is the probability density that the histogram of the finite distribution approaches as the number of samples becomes very large.
The practical implication of the distinction is shown in Figure 2 (see June 2000 issue of EE) in which 20 histograms of data output from Excel’s random number generator have been superposed. The 20 histograms, the average of five, and the average of all 20 are shown in gray, black, and red, respectively. A very large number of data points must be accumulated before their average bears a good resemblance to the theoretical PDF curve.
Each histogram has 142 bins, 0.05 s wide, corresponding to the -3.5 s to +3.5 s range of the variable c. The bins contain the number of values in the complete 10,000-point data set that is between the upper and lower bin limits. For example, in the fourth histogram, there are 185 data points with values between 0.35 and 0.40. Plots are made to correspond to the scaling in Figure 1 by dividing the number in a bin by the width of the bin and by the total number of points.
The cumulative distribution function (CDF) is defined by Equation 2 as the integral of Equation 1 or the area under the PDF curve. If the PDF expresses the probability of a particular value c appearing in an infinitely large data set, then the CDF shows the probability that a value will be less than or equal to c. In practice, because the set of data samples is finite, with quantized power resolution, the integral is replaced by a summation. This is the definition used by instruments that process sets of discrete data points.
For Figure 3 (see June 2000 issue of EE), the probability of a value being less than 3.5, for example, is very nearly 1.0. Virtually all of the area under the PDF curve lies to the left of 3.5. Similarly, it’s easy to see that exactly half the PDF area lies to the left of µ, in this case 0. So, the CDF curve passes through the point probability = 0.5 and c = 0.0.
The complementary cumulative distribution function (CCDF) is simply
CCDF = 1 – CDF
The vertical axis represents the probability that a value is greater than or equal to c. A practical example will demonstrate the usefulness of the CCDF.
Assume that power in units of decibels above 1 mW (dBm) is a normally distributed random variable with a mean of -10 dBm and a standard deviation of 5 dBm. Figure 4 (see the June 2000 issue of EE) shows the histogram of 10,000 power samples labeled in dBm as well as in units of s.
The corresponding CCDF is shown in Figure 5 (see the June 2000 issue of EE). The shaded part of the figure usually is not displayed because maximum rather than minimum crest factors are of interest. The entire curve has been shown here to help clarify why the highest cumulative probability included in a typical plot may only be 50%, for example. The lowest of the three sets of X-axis labels is scaled in dBm relative to the mean. Subtracting the mean in decibels is equivalent to dividing powers measured in watts.
The curves diverge at high positive values because of the relatively small number of samples. However, any finite distribution will have a highest point, and in Figure 5, it’s about 3.4. The red curve becomes vertical at 3.4, indicating the highest value. On a linear Y axis, rather than the logarithmic one used here, the end of the red curve would intersect zero probability at the crest factor, about 16.5 dB.
The intersection of the CCDF with levels of probability other than zero is interpreted as the percentage of time that the peak-to-average ratio will be above some value. For example, from Figure 5, 1% of the time the peak-to-average ratio will be above about 11.5 dB.
The CCDF of normally distributed random noise is important, but it’s only a reference. In Figure 6, two different combinations of CDMA channel codes have been used. Curve A results from choosing eight codes at random while curve B corresponds to choosing the eight codes giving the highest crest factor.
CDMA Walsh codes consist of 64 bit locations that may be a 1 or a 0. The codes are chosen to be orthogonal. This means that several carriers at the same frequency, each modulated by a different Walsh code, can be sorted out after they are mixed together. On the downside, Walsh codes are only finite sequences, and there are times that 1s from different codes can coincide, causing a greater peak power demand for a base-station transmitter, for example.
Figure 6 shows this effect. For the system being measured, curve B can be up to 2 dB higher than curve A and have a peak-to-average ratio of about 11 dB for 0.1% of the time. The proposed wideband CDMA (W-CDMA) system can have even greater crest factors.
High crest factors imply a need for greater amplifier linearity. If a system works well most of the time but fails occasionally, the failure can be caused by signal compression at high peak power levels. Unless the CDMA peaks are preserved, separate data channels will not be received properly.
This is an important point to make in evaluating a power meter for CDMA work. Some of the higher power peaks occur very infrequently. The meter must continuously acquire data, possibly for several seconds, to provide an accurate estimate of the signal’s PDF and CCDF. The occasional peaks are important, and by implication, the meter must be able to process large amounts of data in real time.
Sensing the Power
Histograms, CDFs, and CCDFs are generated from peak power measurements. However, average power traditionally has been one of the most commonly required RF measurements.
Gurpreet Kohli, vice president of sales and marketing at Boonton Electronics, said there are so many different sensors available from each manufacturer because the averaging time constant of the sensor often is tuned to specific types of modulation. He felt that the provision of many modes of power measurement in modern meters results from users’ familiarity with the meaning of average power on one hand and a lack of an agreed, rigorous definition of peak power on the other hand.
It can be difficult to measure the power of a digitally modulated signal. Steve Reyes, marketing manager at Giga-tronics, said, “When using a thermal sensor, we must wait for the sensor to settle to the average power level of the modulated waveform. This often can take multiple cycles of the modulation.
“A diode sensor samples the power envelope and provides average power by integrating the accumulated sam-ples,” he continued. “The diode sensor must be able to track the power envelope. If it does not have a video bandwidth high enough to do this, the sensor will provide up to a few tenths dB offset error.”
Diode sensors are much faster than thermocouples, but for inputs with even brief peaks above about -20 dBm, the diode’s output becomes nonlinear. Three approaches have been developed to cope with this problem.
- The diode input/output transfer curve can be linearized for continuous wave (CW) modulation signals. Because averaging is performed before the sensor data is processed, signals other than CW will produce incorrect averages that cannot be corrected. Typically, these types of sensors may have a large dynamic range from 80 to 90 dB, but they are of limited use.
- Peak sampling meters digitize the diode output and correct each sample before further processing. In this way, the diode nonlinearity can be removed and a large dynamic range retained. The full characteristics of the signal are captured and can be processed to yield the required statistical information.
- Recently, sensors have been developed that combine two or more sets of diodes and attenuators. The idea is to cover a wide dynamic range linearly by using only the linear part of the diode circuits. For example, if two parallel paths are used, one may have a 40-dB attenuator in series with the diode. As a result, an 80-dB dynamic range could be covered from -60 to +20 dBm, assuming distortionless, automatic switching occurred between the two paths at the -20-dBm level.
Angus Robinson, market segment manager at Anritsu, explained, “By cascading standard diode pairs in a single sensor and inserting differing attenuation values into the paths to each diode pair, it is possible to design a sensor that always has at least one diode pair operating in its square law region. This technique gives excellent low power accuracy and measurement speed.”
In contrast, Mr. Robinson said that meters averaging sampled data points to determine average power, “showed very poor stability and accuracy below -40 dBm.”
Irrespective of the exact details of the fast diode sensor used, peak power measurements relate to sampling. Because power is a scalar quantity, signals can be undersampled at a rate lower than the highest frequency of the modulating waveform. Eventually, the peak of a repetitive modulation signal will be acquired. Mr. Reyes said that Giga-tronics uses random sampling to ensure that aliasing does not occur when undersampling.
If the modulation is not repetitive, then the signal must be oversampled to capture the peak within a given time span. Even so, to be certain that you have acquired the peaks, sampling must be continuous and at a rate about five times the signal bandwidth. This means that diode sensors with large video bandwidths are required.
Return to EE Home Page
Published by EE-Evaluation Engineering
All contents © 2000 Nelson Publishing Inc.
No reprint, distribution, or reuse in any medium is permitted
without the express written consent of the publisher.
June 2000