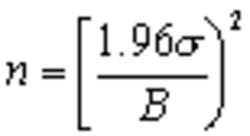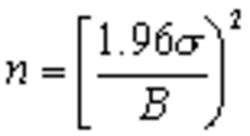Jitter is defined as the unwanted variation in the timing of successive events. That statement’s broad wording applies to a range of pulse-edge positions relative to a reference clock as well as variation among the widths of a series of pulses. Jitter denotes unintentional modulation of edge position, pulse width, frequency, rise time, or other timing parameters typically caused by random noise or deterministic noise such as crosstalk (Figure 1).
Wander can be defined in the same terms as jitter but is much slower. Timing variation that occurs at a rate below 10 Hz is termed wander; above 10 Hz, it’s jitter.
For example, if the output of a 10-MHz oscillator were examined carefully, some of the cycles would be longer than 100 ns and some shorter. The difference between the longest and shortest cycles is the peak-to-peak jitter.
A histogram of the variation in cycle length reveals the nature of the jitter and may help identify its source. If random noise is the main cause, the histogram will have the usual bell shape of a Gaussian or so-called normal distribution. You may have to make many hundreds or thousands of measurements to obtain a histogram that looks like the classical textbook curve because the disturbance is random.
Figure 2 shows the histogram of a bimodal distribution. The two peaks at the same height denote there is an equal probability of a cycle being long or short, perhaps caused by crosstalk from a sine or square-wave source. The width of either of the normal distributions depends on the amplitude of the random jitter (RJ) adding to the deterministic crosstalk.
The histogram will have the same shape whether it is displaying the actual measured width of each cycle or the difference between each width and the nominal 100-ns width. Only the mean of the distribution will change from 100 ns to 0.0 ns.
Deterministic noise is bounded in comparison to unbounded random noise. This means that the effect of deterministic noise won’t greatly change the characteristics of a jitter histogram as more and more samples are acquired.
On the other hand, although the shape of a jitter histogram corresponding to random noise may not change perceptibly, higher peak jitter will occur as more samples are captured. Deterministic jitter does not behave in this way because the magnitude of crosstalk, for example, is limited by the amplitude of the source and the coupling mechanism.
The probability that a particular value will occur is related to sigma (s), the standard deviation of the distribution. Any normal distribution will have 68.26% of the measurements lying within a 1-s wide band. Extending the region to 2 s includes 95.4%, and going farther out to 3 s accounts for 99.73% of all members of the distribution. Although a normal distribution theoretically is unbounded, the frequency of occurrence of very large or very small values is extremely low—10-s values account for only 1.973 ´ 10-21% of the population.
Nevertheless, the probability of occurrence of extreme values is finite. Unfortunately, because of the multigigahertz clock rates that have become common, achieving an enormous number of clock cycles is not that difficult. There are 3.15 ´ 107 seconds in a year, so about 1017 clocks will be produced by a 3-GHz clock in a year. During this time, you could reasonably expect to see at least one occurrence of an 8-s value.
Measurement Choices
Oscilloscopes
One way to measure a signal with an oscilloscope is to trigger on the 50% crossing of the positive edge and record the time of the 50% negative-edge crossing. This method is intuitive and relatively fast but error prone. Because the trigger circuitry contributes jitter, the measurements of the negative-edge timing include trigger jitter as well as signal jitter.
Measuring between the positive and negative edges of a pulse that occurs after the trigger eliminates the error associated with trigger jitter. Each pulse-width measurement represents the sum of the nominal pulse width and the jitter at that point in the pulse stream.
By averaging all of the pulse measurements, you can determine the mean pulse width. If you capture a large number of contiguous pulses in a single acquisition, subtracting the mean from each measurement will produce an estimate of jitter as a function of time.
A real-time analog scope shows jitter as a series of ghosted lines or a blurring where ideally there should be one, thin edge of a signal. This type of display can be helpful during troubleshooting, assuming you can achieve the required balance of trigger rate, trace brightness, and focus. Remember the viewing hoods used when looking for infrequent fast artifacts?
Digital storage oscilloscopes (DSOs) sample input signals and attempt to interpret the acquired data as meaningful waveforms. Physical electronic signals are well-behaved, single-valued functions of time, so DSOs usually display a good waveform likeness except for sample-rate-related aliasing.
Only recently have DSO signal acquisition rates approached those of analog scopes, allowing you to enjoy a more realistic display of waveform modulation including jitter. At the same time, waveform appearance remains compromised by the limited resolution of typical DSO raster-scan display devices and the resulting spatial quantization.
Despite a DSO’s not-quite-real-time-quality waveform presentation, the sampled data points correspond directly to the actual input signal. If you use your DSO for jitter investigation, this fact alone may make the instrument worthy of the marketing-bestowed real-time scope moniker.
To simplify the specification of DSO accuracy, Tektronix uses a Delta-Time-Accuracy equation that accounts for all sources of time measurement errors. For the TDS7404 DSO, the accuracy is given by Equation 1. The 3.5-ppm portion of the equation relates to the time-base oscillator accuracy, and the 0.06/sample rate accounts for all other errors including vertical noise and sampling-related errors.
Accuracy = 0.06/SR + 3.5 ppm × measurement period (1)
For example, the accuracy of a single 10-ns period measurement made at a 10-GHz sample rate is 6 ´ 10-12 + 3.5 ´ 10-14 = 6.035 ps rms. For very short times, the scope’s internal noise sources dominate clock oscillator inaccuracies. On the other hand, for a 10-ms pulse sampled at a 10-MHz rate, the accuracy is 6 ´ 10-9 + 3.5 ´ 10-8 = 41 ns, governed by the oscillator term.
Very long memories in modern DSOs enable you to maintain a high sample rate even for relatively slow signals. This means that you can avoid the poor accuracy that would result from applying Equation 1 to the measurement of a 1-s period at a 1-kHz sample rate, for example. The error in this case is 63.5 µs or 18 times worse than the worst-case oscillator specification.
Long memories support the capture of a large number of successive events. By examining the timing variations from pulse to pulse within one long acquisition, you can develop a display of jitter vs. time, a so-called time vs. time display.
If the jitter source is deterministic, such as crosstalk from a switching power supply, the periodicity of a jitter vs. time plot will reveal it. Deterministic jitter (DJ) will distort the histogram display as shown in Figure 2, but unless DJ is caused by a simple waveform, the nature of the modulation may be more obvious in a jitter vs. time presentation than in a histogram.
DSOs from LeCroy, Agilent Technologies, and Tektronix provide standard or optional measurement and histogram functions that analyze successive pulse widths within a long acquisition. So-called cycle-to-cycle statistics can be derived to help pinpoint the source of any unwanted jitter that may be present. In addition, the time-tested Amherst M1™ Time Interval Measurement System Software supports extensive jitter measurements for DSOs from all three manufacturers.
Timing Interval Analyzers (TIAs)
Another approach to jitter measurement focuses on the constituent parts that comprise jitter. If the DJ components can be identified, the part that remains is random jitter and will follow the well-known behavior of a normal distribution. In particular, if the right and left tails of a histogram can be confirmed to correspond to normal distributions, then it is possible to infer the probability of occurrence for extreme values greater and smaller than the actual acquired samples.
This thesis underlies several patents acquired by WAVECREST that relate to the separation of RJ and DJ and has application in bit error rate testing (BERT). As previously stated, the 3-GHz clock had a probability of 1 part in 1017 of producing an 8-s error in a year. Even if an error rate of only 10-12 is required, corresponding to about 7 s, a brute-force test at a 100-MHz clock rate still will take at least 10,000 seconds or about three hours.
By carefully fitting normal curves to each end of the data distribution, WAVECREST claims to be able to predict the likelihood of occurrence of high sigma values from a minimal number of actual data points. This greatly speeds up BERT, and many comparisons of test results have confirmed the validity of the method.
Approaching the jitter problem from this direction highlights the statistical independence of each sample. To improve independence, the WAVECREST SIA-3000 Signal Integrity Analyzer uses a variety of techniques. The clock system consists of a very low drift, ovenized, 10-MHz crystal oscillator to which is phase-locked a 200-MHz, very low phase-noise oscillator.
“Short-term stability of the 200-MHz oscillator output is about 0.1 parts per billion (ppb), and the long-term stability or aging is 150 ppb/year,” said Craig Emmerich, a product marketing engineer at WAVECREST. “To further ensure statistical independence, we randomize the hold-off time between measurements. The overall measurement rate is about 3.3 MHz, consisting of a burst of 16 measurements taken at the end of a random 4- to 5-µs period.”
Attaining Subpicosecond Measurements
Both TIAs and DSOs claim picosecond accuracy although neither instrument uses a terahertz clock. Interpolation and averaging are the magic ingredients.
Interpolation
Even though a DSO may have a 10- or 20-GHz clock rate, these high speeds only correspond to 100- or 50-ps sample periods, respectively. But if an accurate interpolation can be performed to find the 50% level crossing time for each edge in a multiple-pulse acquisition, the measurement resolution can be improved by at least an order of magnitude. Typically, these crossings will lie between actual samples so all values used later to develop a statistical view of the jitter being examined will have to be interpolated by firmware or software.
In a TIA, sampling is asynchronous as it is in a DSO, but the leading-edge 50% point of a pulse starts an interpolation timer that directly measures the time from the leading edge of the pulse to the next clock pulse. Similarly, the trailing edge of the same pulse starts a second timer that ends on the following clock edge.
The actual pulse width is found by suitably combining the values of the timers and the number of elapsed clock periods. In reality, because of the practical difficulty of starting and stopping analog timers quickly, the timers may be constrained to run for a minimum of one clock period and the pulse-width computation adjusted accordingly.
WAVECREST’s SIA-3000 interpolators have a resolution of 200 fs, so this type of analyzer directly acquires very high-resolution data. Because of the clock stability, the data has high relative accuracy.
Averaging
Equation 2 determines the number of samples n required to achieve a level of accuracy B given the standard deviation s of a distribution.
Because the standard deviation is defined as the rms sum of the differences between the actual values and the mean, the accuracy of sigma depends on the number of samples taken. The mean is the average of all the samples.
“As the number of measurements increases, the accuracy of a statistical quantity such as standard deviation improves as the square root of the number of measurements,” explained Ken Johnson, a LeCroy product manager. “In general, the measurement accuracy is relative but can be calibrated if a precision source with known jitter is available.
“Because jitter is statistical in nature, you can express accuracy using statistical confidence levels,” he continued. “For example, the LeCroy J-260 Jitter Analyzer has an accuracy specification of 1-ps rms at a 3-s (99%) confidence level.”
The values given in Table 1 (see below) demonstrate Equation 2 in action. An Excel spreadsheet was constructed to model the 10-MHz oscillator example. Values from a normal distribution with s = 1 were added to the nominal 100-ns cycle period.
The three STANDARD DEVIATION columns show that Equation 2 gives a conservative estimate of the number of samples required to ensure a certain accuracy in sigma. The five MEAN columns confirm the convergence of the mean to 100 as well as the increase in peak-to-peak jitter as the number of samples increases. A positive value greater than 4 s occurred at sample number 3834: 104.009344. In this particular distribution, the smallest minimum value of the 10,000 samples was logged at sample number 57: 96.15829.
These columns show the effect of truly random values. By chance, the accuracy of the mean derived from 10 samples is far better than that determined from 100. It just emphasizes the need to include many thousands of samples to ensure that your conclusions won’t vary appreciably the next time you run the test.
Summary
A DSO can give you quick insight into the nature of signal jitter. It can provide true cycle-to-cycle statistics and histograms, and some models have special jitter displays such as LeCroy’s JitterTrack.
A DSO is limited in the number of samples it can acquire, however, even with the 10-MS and larger memories available today. Nevertheless, 100,000 samples, for example, constitute a large enough distribution to represent the nature of most problems. On the other hand, the acquisition of millions of truly independent events may be better done by a TIA such as the WAVECREST analyzer.
Finally, if you must determine jitter in a production test environment and feel that neither a TIA nor a DSO is exactly right for the job, consider the LabVIEW-compatible version of Amherst’s M1 software. The package provides statistical analysis of files of data from your custom acquisition system.
Whatever the source of the data samples, the absolute accuracy will constrain the analysis accuracy. Beware of rms values and numerical displays such as s = 12.145 ps. Remember that for about 0.5% of the time the peak value of a quantity will be more than 3´ the rms value. How accurate is a derived measurement result? Have enough samples been included to support femtosecond accuracy? How many of the digits are really significant?
If these concerns are important to your work, spend enough time learning about the very complicated subject of jitter so you can choose the best solution for your application.
Return to EE Home Page
Published by EE-Evaluation Engineering
All contents © 2001 Nelson Publishing Inc.
No reprint, distribution, or reuse in any medium is permitted
without the express written consent of the publisher.
January 2002