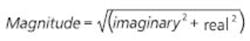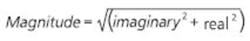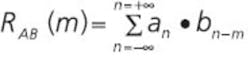With a good DSA, analyzing the sound of one hand clapping is not a problem.
A dynamic signal analyzer (DSA) is used to investigate signals representing forces and motions. In this context, the word dynamic has a precise mean-ing distinct from the usual synonyms such as spirited or energetic. Dynamics is the branch of mechanics concerned with the motions of material bodies under the action of given forces. It follows that a dynamic system is a group of interacting mechanical components and forces.
Dynamic systems clearly have a time element associated with them, although many effects are better understood by their frequency spectrum. For example, noises within a car may be of the squeak or rattle variety. Because this type of problem is so common, especially in dashboard assemblies, it�s become a standard procedure for auto manufacturers to test for buzz, squeak, and rattle. Similarly, there�s also noise, vibration, and harshness testing.
DSAs sample their input signals in the time domain but provide comprehensive fast Fourier transform (FFT)�based frequency-domain capabilities. Signal conditioning includes selectable anti-alias filtering in addition to basic facilities such as multiple input ranges. Dynamic signals often are AC coupled, which eliminates DC offset and drift problems. A DSA also may contain a signal source that you can use to excite the system under test.
Because even a small amount of energy at the wrong frequency is undesirable, a DSA�s dynamic range is an important specification. The term dynamic range refers only to the ratio of the largest to smallest signals handled and has no other connection to dynamic systems.
A high-resolution ADC preserves the dynamic range of the analog input circuitry better than one with less resolution and is absolutely necessary if the DSA is to have a low noise floor. The highest commonly available resolution is 24 b, and many DSAs have this resolution. In addition to supporting a large dynamic range, high resolution also is more forgiving of a suboptimal gain setting.
Unfortunately, most high-resolution ADCs are of the delta-sigma type and include a very high-order digital filter. The extremely sharp filter cutoff in the frequency domain creates artifacts in transient time-domain signals. Obviously, these are not part of the real signal and add to the data acquisition system errors.
If the signal bandwidth presented to the ADC has been reduced by an analog anti-alias filter, the effect can be avoided. However, it is economically advantageous to use one fixed-frequency analog anti-alias filter ahead of a delta-sigma ADC running at a high sample rate. At lower sample rates, further filtering occurs via digital decimation with the attendant time-domain artifacts. The sidebar accompanying this article describes a digital method that eliminates the artifacts, and a patent has been applied for this technique.
Beyond basic characteristics, DSA feature sets and their implementations vary widely. Some vendors, such as National Instruments (NI), provide the constituent parts of a DSA in the form of data acquisition boards and data processing software. The type 446x and 447x products have from two to eight input channels, a 3-dB bandwidth up to about 80 kHz, and built-in anti-alias filtering. You need to use the company�s Sound and Vibration Toolkit software to perform signal analysis.
In contrast, the 16-b NI 455x data acquisition boards have a built-in DSP. This means that spectral analysis is performed in hardware much more quickly than with a software-based approach. The board interface is via the dedicated NI-DSA instrument driver, and you must select the algorithms that will run on the DSP.
The usual advantages for modular, software-based instruments apply to this type of approach: a high degree of flexibility and the capability of higher performance with a faster PC. Against these positive factors, the user must do much more instrument development work, although having commonly used algorithms bundled as a software toolkit helps.
Several PC-based products include a separate data acquisition chassis with DSP processing. Instrument interface functions and display of analysis results are handled by the PC, but the combination of PC and hardware behaves as an integrated turnkey solution.
Other manufacturers package their DSAs as stand-alone instruments similar to spectrum analyzers or DSOs. The functionality may be limited to that originally shipped, or you may have the option of downloadable field upgrades and custom analysis routines. Upgradeability is a capability worth looking for because you probably will be using a newly purchased DSA for many years.
Physical phenomena usually are below 100 kHz in frequency and don�t change a lot from year to year, so a mature instrument design may not be a bad thing: The manufacturer should have corrected any early production problems, for example. Also, to keep up with the competition, the instrument software will have been periodically enhanced with new features and perhaps more efficient algorithms.
Frequency-Domain Tools
FFT
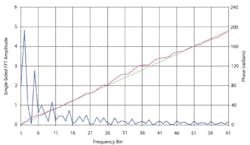
Most DSAs use the FFT to produce a frequency-domain representation of data acquired in the time domain. For a block of N = 2n data points, the corresponding single-sided spectrum will contain N/2 discrete frequency lines spaced Fs/N apart, where Fs is the sampling frequency. The first line is at DC and the last at Fs/2 – Fs/N. For example, if 2,048 points are acquired at a 1,024-Hz rate, the FFT will produce 1,024 lines spaced 0.5 Hz apart extending from DC to 511.5 Hz.
Although many DSA users simply may accept the FFT-based frequency-domain display presented to them, there are many reasons to maintain a healthy skepticism. The FFT assumes that the continuous function of time that has been sampled has a period corresponding to the length of the captured data block. This coherence condition is satisfied if the samples are all unique and an integer number of cycles of the periodic signal fit within the N samples.
A transient signal that decays to zero before the Nth sample is a special case that meets these conditions. Another suitable situation may be created when you can precisely control the sample rate and input signal frequency. In this case, you can achieve coherent sampling if N�Fin = B�Fs where Fin is the input signal frequency and B an odd prime number smaller than N.
For example, if B = 1, exactly one cycle of the input signal will be captured and Fs = N�Fin.The samples all will represent different points on the waveform.
To reduce the ratio of Fs:Fin, a much larger value of B could be used. If B = 211 and N = 4,096, for a 1-kHz input signal, the sampling rate Fs must be 19.412322 kHz. In other words, there will be 19.412322 samples per cycle of Fin, and the samples will represent different points on each of the 211 cycles.
Satisfying the coherence criteria causes all the energy associated with each spectral line to be correctly represented. In general, sampling is not coherent perhaps because you don�t have precise control of the sampling rate but more often because the exact input frequency is unknown. In this case, the energy from one spectral line will become spread across several adjacent lines, an effect called spectral leakage.
To reduce leakage, windowing is required. If an input signal that is not periodic with respect to the sampled data block is convolved with a suitable function in the time domain, it can be made to equal zero at the beginning and end of the data block. There are many different windowing functions, and choosing which to use depends on many factors.
The point of the discussion is not to get into the details of Blackman, Hann, or Hamming windows but rather to explain that the spectrum produced by the FFT depends on much more than just the input signal. The difference between coherent and noncoherent sampling is large, and test results can be misleading if the FFT is indiscriminately applied.
Frequency-Domain Functions
Whatever DSA you may have, it probably includes analysis functions such as linear, cross, and power spectrum; power spectral density; autocorrelation; cross correlation; histogram; probability density functions (PDF); and cumulative distribution functions (CDF). What are these things and what are they used for?
When the FFT function is applied to a series of N time-domain values, it returns the real and imaginary components for N/2 positive and N/2 negative frequency bins. This is a double-sided FFT. To convert to a single-sided spectrum, find the magnitude at each frequency:
Phase can be expressed as phase = arctan [imaginary(FFT)/real(FFT)] where the arctan function needs to operate over the entire range of �? radians.
Starting with the line after the DC line, double the amplitude for all the positive frequency lines and discard the negative frequency lines. The single-sided spectrum represents the peak amplitudes of cosine functions at each frequency bin and with individual phase offsets.
The power spectrum can be computed by multiplying the complex value of the FFT by its conjugate: power is proportional to [real(FFT)+imaginary(FFT)j] � [real(FFT)�imaginary(FFT)j]. Because the inner products cancel when complex conjugates are multiplied
(x+jy) � (x-jy) = x2+y2 = magnitude2
More generally, if the FFT of one time-domain signal Q is multiplied by the complex conjugate of the FFT of another signal R, a cross power spectrum results. Here the inner products do not cancel, so the phase of each line will not be the same as either of the phases of the corresponding lines in Q or R. The power spectrum is the same as the cross power spectrum but with signals Q and R identical. Because of this, the power spectrum also is called the auto power spectrum or the auto spectrum.
The cross correlation of two sets of N samples A[a1, a2,�aN] and B[b1, b2,�bN] at an offset of m samples is defined as
For a real series of N samples and for values of m from -N to +N, cross or autocorrelation gives a resulting waveform twice as long as the original sampled signal.
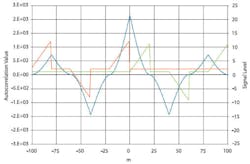
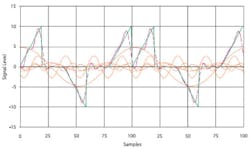
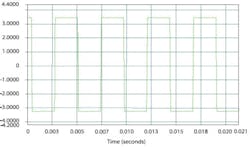
Figure 1 shows an example of autocorrelation. The red and green waveforms represent the same data but shifted vertically away from zero to reduce overlap of the curves and horizontally to demonstrate the sliding action of correlation. This relative horizontal position of the two curves corresponds to the zero value at the left edge of the blue autocorrelation curve where m = -N.
Summing the products of red and green points having the same horizontal value gives a nonzero result as the red waveform is progressively moved to the right with an increasing value of m. The blue peak about one division from the left edge corresponds to the red curve being shifted one division to the right so that its last ramp section and the green curve�s first ramp section coincide. As that shifting took place, the blue autocorrelation sum increased corresponding to the increasing degree of red-green overlap.
The largest peak occurs after N shifts, at m = 0, as it does for any autocorrelation operation. If the signal is periodic, such as a sine wave, there may be other peaks as large, but the autocorrelation value cannot ever be larger than when m = 0 and the curve is exactly aligned with itself. Further shifting causes the degree of overlap to reduce until, after an additional N shifts, the red curve will be completely off the right edge of the graph. This position corresponds to m = +N and the last blue value of zero.
Figure 2a shows the FFT of the same set of N samples and Figure 2b the sum of several frequency components that approximates the original waveform.
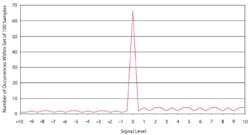
Histograms, PDFs, and CDFs display the relationships among the values of the samples within a group. For example, a histogram generated from the set of N samples shown in Figure 1 is displayed in Figure 3. It�s intuitive from the waveform in Figure 1 that the value zero occurs most often, and this is clearly shown in Figure 3. Also, because a single cycle of the waveform contains two positive ramps and only one negative ramp, positive values occur twice as often.
PDFs and CDFs generally are used to help understand noise-like signals rather than the well-defined waveform in Figure 1. For example, the distribution of power at different frequencies describes a vibration test and often is presented as a power spectrum density (PSD) display. Of course, a swept sine source could be used, which would be very predictable. More often, and especially in pneumatic actuator driven HALT/HASS chambers, vibration appears to be random but with a predetermined distribution.
A PSD is a density function with units of power per hertz, usually expressed as g2/Hz. A CDF is the integral of a PDF. Integrating the area under a PSD curve displays the percentage of the total power that is applied below a certain frequency. For example, in a normal distribution, 50% of the power exists for frequencies less than the mean because the distribution is symmetrical.
In general, distributions used in real vibration testing concentrate energy within defined frequency bands to simulate the stresses experienced in actual use. In the case of a pneumatic actuator-driven vibration table, significant energy simply is not produced outside of a frequency band from a few hundred to a few thousand hertz.
Summary
It should be clear from the many specialized functions DSAs provide that it�s difficult to accomplish detailed vibration analysis with basic data acquisition tools. If you�re investigating vibration, you need a DSA or at least the appropriate analysis and display software. Manufacturers of DSAs tend to use standard mathematical terms, although the names of the instruments themselves vary. The DSA name is common, but the product also is called a spectrum analyzer, which emphasizes the frequency-domain aspect of many of the analysis functions.
Ripple Elimination in Delta-Sigma Systems
by Gordon Shen, LDS-Dactron, LDS Test and Measurement
Data acquisition systems apply anti-alias filtering before the signal is converted from analog to digital. In almost all systems, the sampling rate can vary greatly, so the cutoff frequency should adapt accordingly.It is very difficult and sometimes even impossible to adapt the cutoff frequency of a high-order analog filter. So digital decimation often is used to vary the sampling rate. With this approach, the hardware sampling rate is fixed at a relatively high value, and the cutoff frequency of the analog filter does not need to adapt.
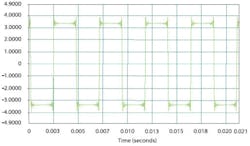
The sharp decimation filter causes the step response to have significant overshoot as shown in Figure 4. The ripple can easily be as high as 10% of the step amplitude, causing measurement accuracy issues.
Since linear phase characteristics are preserved with an FIR filter, it has the potential to overcome certain limitations of a digital Bessel filter. However, an FIR filter usually has a very sharp transition band. Indeed, in the past, engineers have strived to make the transition band as sharp as possible, but to eliminate transient ripples, we need a slow transition band.
An FIR filter with a few taps creates the desired effect. Figure 5 represents the step response with a four-tap FIR ripple elimination filter, showing that the overshoot has been eliminated. The result is as good as an analog Bessel filter.
Figure 5. Delta-Sigma Transient Response With Added Linear-Phase FIR Filter
The ripple elimination filter overcomes the poor step response of a delta-sigma ADC. Delta-sigma ADCs with ripple elimination filters offer the following benefits relative to acquisition systems using Bessel filters:
� Better Phase Match Between Channels
Because the analog filter is fixed at a relatively high frequency, the phase distortion by capacitor error will be decreased, improving the channel phase match.
� Wider Bandwidth With Same Sampling Rate
If the frequency-domain property is emphasized, the cutoff frequency of the decimation filter can be set at near 0.45 Fs.
� More Versatile
A powerful digital filter can be applied after sampling according to the needs of different applications.
August 2005