Determine MOSFET Junction Temperature And Switching Losses For Various Package Types
This is part of the Ideas for Design Series: Ideas for Design Vol. 1
Download this article as a PDF file
The junction temperature of power MOSFETs is one of the major criteria used to obtain temperature derating curves for power converters. This article describes an improved technique for determining MOSFET junction temperature and switching losses more accurately based on the given thermal resistances and lead and case (package) temperature measurements.
To keep the junction temperature (Tj) within specifications, allowable drain (leads) temperature, (TD), is often calculated as:
TD = Tj – (Pj × θJD) (1)
where Pj is the total heat power generated inside the package (including conduction, switching, and gate losses), and θJD is the junction-to-drain (leads) thermal resistance, which is a package-related parameter provided in the MOSFET’s data sheet. The table shows typical values of θJD for some standard power MOSFET packages.
For example, if a MOSFET in an SO8 package (θJD = 15°C/W) dissipates a Pj of 1 W and must maintain a junction temperature below 125°C, then the measured drain temperature must not exceed 110°C according to Equation 1:
TD = 125°C – (1 W × 15°C/W) = 110°C (2)
Using Equation 1 implies that Pj can be determined under any operational condition and that the total power generated inside the package is dissipated to ambient through the drain leads. In reality, the accuracy of the Pj calculation is relatively low because switching losses in the MOSFET cannot be calculated accurately enough. Also, since a portion of Pj is dissipated to ambient through the MOSFET package, the actual heat flow through the drain leads is smaller than Pj, which presents another source of error.
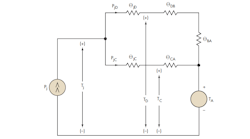
The more accurate technique starts by considering the MOSFET thermal model in the figure, which is a modification of the model used in “Estimating TJ of SO-8 Power MOSFETs”.
According to this model, the total heat generated in the package, represented by current source Pj, flows to ambient through two parallel branches. The first is the junction-drain (leads)-to-PCB-to-ambient route (the “drain” or “lead” branch, labeled PjD) with junction-to-drain thermal resistance θjD, drain-to-PCB thermal resistance θDB, and PCB-to-ambient thermal resistance θBA. The second is junction-to-case (package)-to-ambient (the “case” or “package” branch, labeled PjC) with junction-to-case thermal resistance θjC and case-to-ambient thermal resistance θCA. The model represents the case temperature as TC and the ambient temperature TA by a voltage source.
Applying conventional electrical circuit analysis and Ohm’s law to the model, we obtain the following equations for the heat (PjD and PjC) flowing through the respective drain and case branches:
PjD = Pj/(1 + θD/θC) (3)
PjC = Pj/(1 + θC/θD) (4)
where θD = θJD + θDB + θBA (total drain-branch thermal resistance) and θC = θjC + θCA (total case branch thermal resistance). So, total heat flow Pj is:
Pj = PjD + PjC (5)
Applying Ohm’s law to the combinations of thermal resistances in each branch of the diagram in the figure, we get two equations for junction temperature:
Tj = TD + [(TD – TA) × θjD]/(θDB + θBA) = TD + [(TD – TA) × θjD/θDA] (6)
Tj = TC + [(TC – TA) × θjC)]/θCA (7)
Neither of these equations contain the troublesome heat power term, Pj, and either one can be used to calculate the junction temperature, Tj, as long as the case, drain, and ambient temperatures and the thermal resistances of the package are known.
Consider a typical SO8 power MOSFET with thermal resistances θCA = 380°C/W, θJC = 18°C/W, θJD = 15°C/W, and θDA = 20°C/W (given in “Estimating TJ of SO-8 Power MOSFETs,” again). Substituting these values into Equations 3 and 4, we obtain:
PjD/Pj = 1/[1 + (15 + 20)/(18 + 380)] = 0.92 (8)
PjC/Pj = 0.08 (9)
In other words, 92% of the total power generated in the silicon is dissipated to ambient through the drain, and the remaining 8% is dissipated through the case.
Another important observation is that θCA is much greater than any other thermal resistance in the system, which makes the second term in Equation 7 relatively small. Assuming TC = 125°C and TA = 85°C for the set of parameters given above, Equation 7 gives a junction temperature of:
Tj = 125 + [(125 – 85) × 18]/380 = 126.9°C (10)
This is only 1.9°C greater than the case temperature. Using Equation 6, the drain temperature is:
TD = {Tj + [(TA ×θjD)/θDA)]}/(1+ θJD/θDA) = {126.9 + [(85 × 15)/20)]}/(1 + 15/20) = 108.9°C (11)
So, the drain temperature is 16.1°C lower than the case temperature. This implies that for an SO8 power MOSFET with a θjD on the same order as θDA and with a θCA much greater than θJC, the drain temperature tends to be lower than the case temperature. Also, the plastic case temperature is an accurate representation of the junction temperature.
According to the measured results in “Estimating TJ of SO-8 Power MOSFETs,” the difference between Tj and TC for SO8 packages is typically 1°C to 3°C. If we use the same equations for other MOSFET packages, like PPAKSO8, D2PAK, DPAK, and LFPAK with low junction-to-drain thermal resistances (see the table, again), both the drain and case temperatures are close to the junction temperature. For DirectFET type MOSFETs with metal cases, θJD is even lower and, according to Equation 6, the drain temperature is an accurate representation of the junction temperature.
For a more accurate Tj calculation based on Equation 6, θDA, which is not available from MOSFET datasheets, can be determined. According to the model, junction-to-ambient thermal resistance, θjA, which is provided in datasheets, is a parallel combination of θD and θC resistances and θDA = θD – θjD. Applying this to the model, we can get:
θDA = θjA/(1 – θjA/θC) – θjD (12)
Taking into account that θC is approximately an order of magnitude greater than θjA, Equation 12 can be simplified as:
θDA ≈ (1.1 × θjA) – θjD (13)
Substituting Equation 13 into Equation 6, we get:
Tj ≈ TD + [(TD – TA) × θjD]/[(1.1 × θjA) – θjD] (14)
where all the thermal resistance values are available from the datasheets.
We calculated the junction temperature based on parameters specified on a MOSFET’s datasheet and temperature measurements taken from the component under test conditions. A conventional measurement technique for the drain (lead) and case (package) temperature uses thermocouples placed on the package and on the lead areas.
This technique results in measured temperatures that are lower than actual temperatures for two reasons. First, the thermocouple itself works as a heatsink, cooling the device down. Second, its physical placement is critical when trying to determine the device’s hottest temperature. A more accurate temperature measurement method uses an infrared camera to determine the hottest temperature in the areas of interest (case and lead) without interfering with the heat flow.
Once the junction temperature is determined, the total power generated in the silicon, Pj, can be calculated:
Pj = (Tj – TA)/θjA (15)
where θjA is the junction-to-ambient thermal resistance available from the MOSFET’s datasheet. Pj also can be calculated based on Equation 3 and the junction-to-drain thermal resistance, which is also available from the datasheets:
Pj = [(1 + θD/θC) × (Tj – TD)]/θjD (16)
Although θD and θC are not available from the datasheets, θC is approximately one order greater than θD, so Equation 16 can be simplified as:
Pj ≈ [1.1 × (Tj – TD)]/θjD (17)
After Pj is determined, switching losses, PSW can be calculated in the conventional way:
PSW = Pj – Pdc – Pg = Pj – [Irms2 × RDS(on)] – [Q × Vg × FSW] (18)
where Pdc = conduction (dc) losses, Pg = gate drive losses, Irms = the rms value of the drain current, RDS(on) = the MOSFET on resistance, Q = total gate charge, Vg = peak gate voltage, and FSW = switching frequency. For a square-wave drain current with peak current of Ipk and duty cycle D, Irms2 = Ipk2 × D.
This analysis of the modified thermal model of the MOSFET demonstrates that the hottest spot on the lead and package areas of a power MOSFET is typically a couple of degrees Celsius less than the junction temperature. This hot-spot temperature can be accurately measured by an infrared camera without affecting the device’s heat flow, and the result can be used with the thermal resistance values found in the datasheet to calculate the MOSFET’s junction temperature. Finally, the total power generated inside the silicon and the switching losses can be calculated.
About the Author
Alexander Asinovski
Principal Engineer
Alexander Asinovski is principal engineer at Murata Power Solutions Inc., Mansfield, Mass. He holds BSEE and MSEE degrees from State Technical University, St. Petersburg, Russia, and a PhD from the University of Telecommunications, St. Petersburg. He can be reached at [email protected].