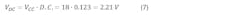Using Unfiltered PWM to Drive High-Power Resistive Loads

Check out more Ideas for Design articles.

Members can download this article in PDF format.

What you’ll learn:

• How to use unfiltered PWM to drive high power loads.
• How to properly set the PWM duty cycle for high power loads.
• How to drive an incandescent lamp using PWM.  

Sometimes it’s necessary to drive a resistive load such as an incandescent bulb or heating element from a DC voltage that’s higher than the nominal load voltage. An example would be driving a 6.3-V, Type 47 bulb¹ from an 18-V DC power supply. A ballast resistor would waste power and cause heating on the printed circuit board (PCB), and a switching power supply would add cost and complexity.

A simple and effective solution is to use the pulse-width-modulation (PWM) output from a microprocessor to drive the load through a switched MOSFET. This article shows how to compute the PWM duty cycle so that the RMS, or effective voltage of the PWM signal, is correct when the load is connected directly to the PWM output.

A common design error is to set the PWM duty cycle to the ratio of the PWM drive voltage and the desired load voltage. This would be correct if a reconstruction filter were used, but without a reconstruction filter, the load would be overdriven and likely damaged.

Leveraging PWM for DACs

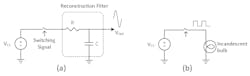
PWM is frequently used to create digital-to-analog converters (DACs), where the reconstruction filter is employed to remove all harmonics of the PWM frequency, leaving only the low-frequency components (Fig. 1).

With the harmonics removed in Figure 1a, the filtered output voltage is:

Equation 1 represents the DC output of reconstructed PWM for the DAC in Figure 1a.

The PWM DAC in Figure 1a is inefficient for delivering power to a resistive load. That’s because while the DC component of the PWM waveform would drive the load, the power in the signal harmonics would be dissipated and therefore wasted by resistor R. The simpler and more efficient approach is to connect the PWM output directly to the load as shown in Figure 1b.²

Supporting an Incandescent Lamp via PWM

Incandescent lamps appear resistive, but the actual resistance is determined by the bulb’s filament temperature.³ For example, a 6.3-V, Type 47 bulb has a DC resistance of about 45 Ω when it glows. This resistance stays constant over a large range of brightness levels. A glowing bulb driven by PWM has the same resistance during the ON part of the PWM waveform as it does when driven by DC.

When driving an incandescent bulb with PWM, the PWM frequency should be high enough so that the bulb filament doesn’t overheat during the ON time. PWM frequencies of 1 to 50 kHz are common. The formulas in this article are accurate for any PWM frequency.

Power Delivered by Unfiltered PWM

The expression for the for the average power in the load when driven by the circuit of Figure 1b is:

where:

P_avg is the power dissipated by the load in watts.

V_RMS is the RMS voltage across the load.

R_load is the load resistance in ohms.

T is the PWM period in seconds.

D.C. is the duty cycle for the PWM (0 ≤ D.C. ≤ 1).

v(t) is the instantaneous voltage across the load.

Equation 2 represents power delivered to the load. Fortunately, the integral in Equation 2 becomes a simple expression by realizing that v(t) is equal to the PWM drive voltage (V_CC) during the ON part of the PWM cycle, and the period (T) cancels in the math. The resulting equation for the average power in the load is:

Equation 3 represents power delivered to the load after simplifying.

Example: Driving a 6.3-V Type 47 Bulb with an 18-V Supply

This example computes the PWM duty cycle that will drive a 6.3-V, Type 47 bulb at the same average power level (brightness) as when it’s driven by a DC voltage of 6.3 V. The strategy is to equate the average power in the bulb for both cases:

Equation 4 equates the power dissipated by the bulb when driven by PWM (left side) and when driven by a DC source (right side). Solving Equation 4 for duty cycle and noting that R_bulb is the same in both cases gives:

Therefore, to drive the 6.3-V, Type 47 bulb at normal brightness with an 18-V PWM output, the duty cycle will be:

A DC voltmeter connected to the PWM output will show the average⁴ reading:

Equation 7 represents the average (DC) value of the 6.3-V_RMS PWM waveform. But if the meter is then set to read AC (and it’s a true RMS meter), it will show 6.3 V_RMS. Therefore, the effective voltage of the PWM waveform is the bulb’s recommended voltage of 6.3 V.

Conclusion: Pulse Width Modulation Simplifies Power Delivery

When PWM is used as a DAC to generate analog waveforms, a reconstruction filter as shown in Figure 1a is required, and the filtered output is the average value of the PWM waveform. However, to deliver power to a resistive load, such as a heating element or an incandescent bulb, the circuit of Figure 1b provides simplicity and power efficiency.

This article showed how to compute the PWM duty cycle that will provide the correct power when the load is connected directly to the switching device.

Check out more Ideas for Design articles.

References

1. Our company makes powered speaker retrofits for antique radios, and our customers will settle for nothing less than the glow, the look, and even the heat from the beloved 6.3-V, Type 47 bulb!

2. If the load isn’t purely resistive, a flyback diode should be placed across the load to prevent damage to the MOSFET.

3. https://en.wikipedia.org/wiki/Incandescent_light_bulb#Current_and_resistance

4. If a reconstruction filter is used, the output will be DC and the voltage will be 2.21 V DC.