What's All This Analog Computing Stuff, Anyhow? (Part 2)

This is part 2 of a 4 part series on analog computing.

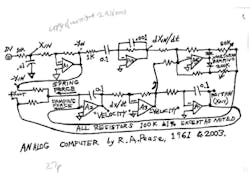
Some time back, I threatened to show you how we used op amps to make useful analog computers. Okay, in the Figure, below, I show a simple six-op-amp circuit to make an analog computer that represents the familiar problem of forced, damped harmonic motion. It simulates the motion of a car over its wheel, when stimulated by a "bump." Equations are available on request.

This simple six-op-amp circuit is an analog computer that addresses the familiar problem of forced, damped harmonic motion.

This computer uses one differentiator to simulate the shock absorber's kick when the wheel hits a bump. In concept, one could use a bunch of differentiators, but they cause more trouble than integrators. So we'll use two integrators—the traditional method. The first integrator represents the way the car's vertical velocity is inversely proportional to its mass and is proportional to the integral of the spring forces plus shock-absorber forces. The second integrator simply states that the position is the integral of the vertical velocity.

If it had no damping coefficient, this circuit would bounce and ring severely, just as your car would bounce a lot if it had no shock absorber. So we add A6 to represent the damping effect of the shock absorber. Apply a little ramp, or step, and the response of the output will do about the right thing. I built one of these in 1960. Did I ever run it? No. Maybe it was too intimidating. But I built this version and it runs quite well.

Note that the two gain paths through A6 can have different coefficients for positive and negative signal velocities. This represents "double-acting" shock absorbers. These could also be made nonlinear.

Now you can make a similar circuit, but with different mass and different spring constants, to represent the rear wheel. Connect them with suitable links to represent the tilt of the car, front to rear, and to couple in the car's longitudinal moment of inertia. Start writing equations—lots of equations.

When this "car" hits a "bump," in the above simulation, does this represent the actual motion of a car? No, not really, as the tire's springiness and lossiness are serious factors in the suspension. So you must engineer another set of 12 op amps to represent the tires. These must link forward and backward between the main spring and the tire systems to get the right damping factors. I mean, the force from the tire does not just act on the springs. The springs act on the tires too. So, you have to pay careful attention to a large number of equations.

This now begins to get close to a good simulation of the car's suspension—-if you get the right "tire inflation." The tire's characteristics are kind of nonlinear, too, when excursions are large—especially when the tire comes off the ground! You really ought to design that into the simulator. (Then if you make a duplicate computer to simulate the right side to match the left side, and add the representation of an "anti-sway bar," you can simulate the "car" hitting "bumps" timed differently on the left side compared to the right. Or, hit a bump during a curve.)

Now, you might be able to do some real engineering on a car, to make various experiments. Then if the modified car matches the modified circuit, you have learned a lot. More on this topic next month.
*January 7, 2002; p. 160.