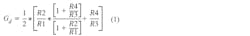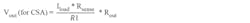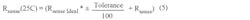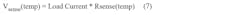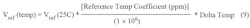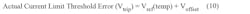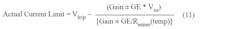This file type includes high-resolution graphics and schematics when applicable.
Recently, an engineer asked for a solution to provide high-side monitoring of a 20-A load with an accurate overcurrent detection threshold of better than 5%. No easily accessible off-the-shelf solutions offer the ability to use a low-value sense resistor with less than 5% accuracy, so why 5%? Would 10% be ok? For a 20-A load, a 10% current limit would cause the trip threshold to be 18 A (min) or 22 A (max), a much wider margin than would be acceptable. What are the factors involved that make 5% so difficult?
Current-Sense Amplifier Basics
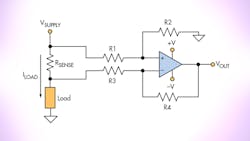
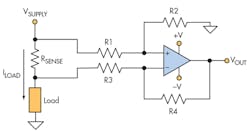
One of several topologies can be employed in the design of a current-sense amplifier. Two common approaches are shown in Figures 1 and 2. Figure 1 depicts an op amp configured as a differential amplifier used to amplify the differential voltage developed across a current-sense shunt resistor. It should also be noted that in some applications, low-side current sensing can be used with limitations (not discussed in this article).
Differential Amplifier as Current-Sense Amplifier
The main limitation of this topology is the resistor ratio match of R1 through R4 that sets the differential gain and the common-mode gain error. Two equations dictate the main source of accuracy errors for the circuit. Equation 1 is the equation for the gain of Fig. 1 and Equation 2 details the common-mode gain error. Equation 3 calculates VOUT for Fig. 1.
When using 1% resistors for R1 through R4 and calculating the errors with worst-case tolerances, the overall error for measuring current would be greater than 5%. Thus, lower-tolerance resistors are needed—at a higher expense. The main drawback of this approach, though, is the requirement for precision resistors with tight tolerance of the ratio values of R4/R3 and R2/R1 to overcome the error sensitivity to higher common-mode voltages.
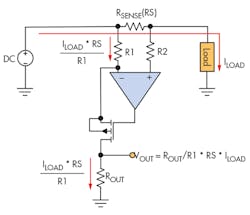
Another common approach (Fig. 2, again) still uses a current-sense shunt resistor to sense the load current. The voltage developed across the sense resistor is then mirrored across R1, and this current is transferred to ROUT. The current-sense amplifier voltage output is:
Rearranging the equation, we see that:
The gain in this configuration is simply the ratio of ROUT/R1, and the ratio error can be easily trimmed out in manufacturing. This topology greatly relieves the requirement for tightly matched resistor ratios that’s required for the circuit in Figure 1. As a result, this approach greatly reduces the common-mode voltage errors found in the differential-amplifier approach. To minimize errors, R2 = R1 to help cancel out any offset error caused by input-bias currents.
Designing a Solution
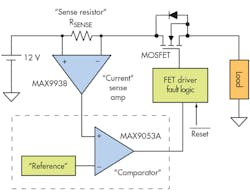
In an effort to design a circuit with accuracy, this design will use the MAX9053A2 comparator with integrated precision reference and the MAX99381 precision current-sense amplifier. The comparator for this solution in Figure 3 has a very fast response time (delay of 450 ns). Response time is critical; this could also impact accuracy and circuit-protection reliability.
Since this article is about accuracy of detecting overcurrent, it will not detail the design and selection of the MOSFET and MOSFET-driver/fault-logic circuit. The design requirements are as follows:
• VSUPPLY = 12 V ±10%, (10.8 V min/13.2 V max)
• Maximum load current = 20 A
• Maximum current limit accuracy at 20 A = ±5% or ±1 A
Choosing the Current-Sense Shunt Resistor
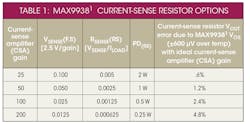
Determining the optimum value for the current-sense resistor (RSENSE) is crucial. Larger RSENSE values increase the series IR voltage drop and power loss, but minimize the effect of the offset voltage error, as shown in Table 1. For designs that require minimal voltage and power loss, use the lowest RSENSE value possible while staying under the overall accuracy target.
Table 1 provides a quick overview outlining the current-sense-amplifier voltage-output error due to current-sense offset voltage and the RSENSE value. The tradeoff here is between choosing a smaller RSENSE at the expense of increasing the gain, and a higher-value current-sense resistor at the expense of using a larger, higher-power current-sense resistor that minimizes the effect of input offset voltage.
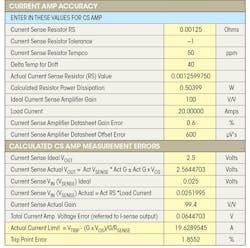
In high-current-sensing applications such as this one, the I2R power losses in RSENSE can be significant. For this design, let’s start with a 0.00125- ⦠sense resistor and current-sense amplifier gain of 100, which is a good compromise between power dissipation and output error. Note that Table 1 was constructed using the desired maximum output current of 20 A and the voltage trip level will be set by the comparator reference voltage of 2.5 V. MAX99381 current-sense amplifier gain options are 25, 50, 100 and 200. Be aware that for a 1.25-V reference, the required gain could be decreased by a factor of two using the same sense resistor. For this example, let’s stay with a 2.5-V reference.
Using an RSENSE value of 0.00125 ⦠(Table 1, again), the ideal linear response for the current-sense amplifier will be 125 mV/A, yielding a current-sense amplifier output of 2.5 V for a 20-A load. It should be noted for the sake of this discussion that available standard-value current-sense resistors may differ from those generated in Table 1.
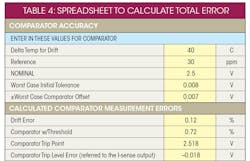
Simply use these values to provide an ideal trip point of 20 A without adjustment. Use the design spreadsheet (see Table 4 below) to enter in other values and quickly recalculate the new trip points. Tables 2 and 3 show the datasheet errors for the current-sense amplifier and comparator. These parameters will be used in the error-budget spreadsheet.
The following equations are used in the spreadsheet. The voltage output for the current-sense amplifier is defined in Equation 4:
In addition, the current-sense-resistor tolerance and drift over temperature will need to be considered when calculating the total error relative to the current-sense amplifier:
Equations needed for calculating errors due to comparator with internal reference:
Equation 11 factors in the actual comparator trip level and the current-sense-amplifier errors and calculates the actual current limit trip point
Using the Design Spreadsheet
When calculating error, spreadsheets can be very helpful and save time when changes are needed. The spreadsheet shown in Table 4 is used to calculate total error based on worst-case errors taken from the datasheet. The root sum of squares (RSS) analysis was not used.
For this spreadsheet, calculate the voltage output of the current-sense amplifiers based on worst gain error, offset error, and sense-resistor tolerance and drift over temperature. Then calculate the worst-case comparator trip level and perform an error calculation based on these two values. The error ideally will be higher than the RSS method. In this example, since the calculated error is less than 5% using worst-case errors, the actual real error is less than the calculated worst-case error. (Note: No error due to CMMR is included; upon datasheet inspection, these errors are insignificant.)
The spreadsheet also includes the errors from the comparator that’s used to determine the overcurrent trip point. It’s highly recommended to view the online AN50953 spreadsheet.
Summary
Current-sense amplifiers can be used in a wide range of applications. When designing with these amplifiers, it’s important to understand the application tradeoffs to minimize the overall measurement error. This article defines the error sources for the current-limit circuit and organizes them in a simple, easy-to-use spreadsheet.
References:
1. MAX9938
2. MAX9053A
3. AN5095
Looking for parts? Go to SourceESB.