Floating-Point Formats in the World of Machine Learning
What you’ll learn:
- Why floating point is important for developing machine-learning models.
- What floating-point formats are used with machine learning?
Over the last two decades, compute-intensive artificial-intelligence (AI) tasks have promoted the use of custom hardware to efficiently drive these robust new systems. Machine-learning (ML) models, one of the most used forms of AI, are trained to handle those intensive tasks using floating-point arithmetic.
However, because floating-point formats have been extremely resource-intensive, AI deployment systems often rely on one of a handful of now-standard integer quantization techniques using floating-point formats, such as Google's bfloat16 and IEEE's FP16.
Since computer memory is limited, it's not efficient to store numbers with infinite precision, whether they’re binary fractions or decimal ones. This is due to the inaccuracy of the numbers when it comes to certain applications, such as training AI.
While software engineers can design machine-learning algorithms, they often can't rely on the ever-changing hardware to be able to efficiently execute those algorithms. The same can be said for hardware manufacturers, who often produce next-gen CPUs without being task-oriented, meaning the CPU is designed to be a well-rounded platform to process most tasks instead of target-specific applications.
When it comes to computing, floating-points are formulaic arithmetic representative of real numbers that are an approximation to support a tradeoff between range and precision, or rather tremendous amounts of data and accurate outcomes. Because of this, floating-point computation is often used in systems with minimal and large numbers that require fast processing times.
It's widely known that deep neural networks can tolerate lower numerical precision because high-precision calculations are less efficient when training or inferencing neural networks. Additional precision offers no benefit while being slower and less memory-efficient.
In fact, some models can even reach higher accuracy with lower precision. A paper released by Cornell University attributes to the regularization effects of the lower precision.
Floating-Point Formats
While there are a ton of floating-point formats, only a few have gained traction for machine-learning applications as those formats require the appropriate hardware and firmware support to run efficiently. In this section, we will look at several examples of floating-point formats designed to handle machine-learning development.
IEEE 754
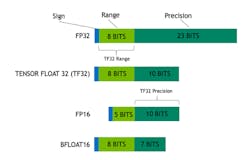
The IEEE standard 754 (Fig. 1) is one of the widely known formats for AI apps. It’s a set of representations of numerical values and symbols, including FP16, FP32, and FP64 (AKA Half, Single and Double-precision formats). FP32, for example, is broken down as a sequence of 32 bits, such as b31, b30, and b29, all the way down to zero.
A floating-point format is specified by a base (b), which is either 2 (binary) or 10 (decimal), a precision (p) range, and an exponent range from emin to emax, with emin = 1 − emax for all IEEE 754 formats. The format comprises finite numbers that can be described by three integers.
These integers include s = a sign (zero or one), c = a significand (or coefficient) having no more than p digits when written in base b (i.e., an integer in the range through 0 to bp − 1), and q = an exponent such that emin ≤ q + p − 1 ≤ emax. The format also comprises two infinites (+∞ and −∞) and two kinds of NaN (Not a Number), including a quiet NaN (qNaN) and a signaling NaN (sNaN).
The details here are extensive, but this is the overall format of how the IEEE 754 floating-point functions; more detailed information can be found at the link above. FP32 and FP64 are on the larger floating-point spectrum, and they’re supported by x86 CPUs and most of today's GPUs, along with the C/C++, PyTorch, and TensorFlow programming languages. FP16, on the other hand, isn't widely used with modern processors, but it’s widely supported by current GPUs in conjunction with machine learning frameworks.
Bfloat16
Google's bfloat16 (Fig. 2) is another widely utilized floating-point format aimed at machine-learning workloads. The Brain Floating Point Format is basically a truncated version of IEEE's FP16, allowing for fast, single-precision conversion of the 754 to and from that format. When applied to machine learning, there are generally three flavors of values, including weights, activations, and gradients.
Google recommends storing weights and gradients in the FP32 format and storing activations in bfloat16. Of course, the weights also can be stored in BFloat16 without a significant performance degradation depending on the circumstances.
At its core, bfloat16 consists of one sign bit, eight exponent bits, and seven mantissa bits. This differs from the IEEE 16-bit floating-point, which was not designed with deep-learning applications in mind during its development. The format is utilized in Intel AI processors, including Nervana NNP-L1000, Xeon processors, Intel FPGAs, and Google Cloud TPUs.
Unlike the IEEE format, bfloat16 isn’t used with C/C++ programming languages. However, it does take advantage of TensorFlow, AMD's ROCm, NVIDIA's CUDA, and the ARMv8.6-A software stack for AI applications.
TensorFloat
NVIDIA's TensorFloat (Fig. 3) is another excellent floating-point format. However, it was only designed to take advantage of TensorFlow TPUs built explicitly for AI applications. According to NVIDIA, "TensorFloat-32 is the new math mode in NVIDIA A100 GPUs for handling the matrix math also called tensor operations used at the heart of AI and certain HPC applications. TF32 running on Tensor Cores in A100 GPUs can provide up to 10X speedups compared to single-precision floating-point math (FP32) on Volta GPUs."
The format is just a 32-bit float that drops 13 precision bits to run on Tensor Cores. Thus, it has the precision of the FP16 (10 bits), but has the range of the FP32 (8 bits) IEEE 754 format.
NVIDIA states that TF32 uses the same 10-bit mantissa as the half-precision FP16 math, which is shown to have more than enough margin for the precision requirements of AI workloads. TF32 also adopts the same 8-bit exponent as FP32, so it can support the same numeric range. That means content can be converted from FP32 to TF32, making it easy to switch platforms.
Currently, TF32 doesn’t support C/C++ programming languages, but NVIDIA says that the TensorFlow framework and a version of the PyTorch framework with support for TF32 on NGC are available for developers. While it limits the hardware and software that can be used with the format, it’s exceptional in performance on the company’s GPUs.
Summary
This is just a basic overview of floating-point formats, an introduction to a larger, more extensive world designed to lessen hardware and software demands to drive innovation within the AI industry. It will be interesting to see how these platforms evolve over the coming years as AI becomes more advanced and ingrained within our lives. The technology is constantly evolving, so too must the formats that make developing machine-learning applications increasingly efficient in software execution.
About the Author
Cabe Atwell
Technology Editor, Electronic Design
Cabe is a Technology Editor for Electronic Design.
Engineer, Machinist, Maker, Writer. A graduate Electrical Engineer actively plying his expertise in the industry and at his company, Gunhead. When not designing/building, he creates a steady torrent of projects and content in the media world. Many of his projects and articles are online at element14 & SolidSmack, industry-focused work at EETimes & EDN, and offbeat articles at Make Magazine. Currently, you can find him hosting webinars and contributing to Electronic Design and Machine Design.
Cabe is an electrical engineer, design consultant and author with 25 years’ experience. His most recent book is “Essential 555 IC: Design, Configure, and Create Clever Circuits”
Cabe writes the Engineering on Friday blog on Electronic Design.