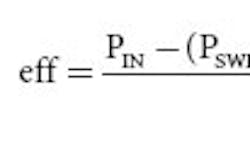Boost Converter Efficiency Through Accurate Calculations

Portable battery-operated electronic equipment is becoming packed with more features requiring larger amounts of power, leading to decreased operating times between battery charges.

Innovations such as dynamic backlight control, where the liquid crystal display's (LCD) backlight power is reduced based on screen content, and automatic voltage scaling, where a microprocessor's frequency and supply voltage are reduced based on computing time requirements, help to gain back those lost milliwatts. This milliwatt level of lost power is important considering the relatively low amounts of power consumed by a typical electronic device, and the small battery capacities that can often be rated at 1000 mAh or less. Essentially, everywhere that power loss can be accounted for helps in optimizing the design and aids in extending battery life.

One contributor to power loss in portable electronic devices is the inductive boost-switching regulator. These types of converters are typically used to power white light-emitting diodes (LEDs) in back-lit LCDs, organic LED panels, high-current flash LEDs, or even audio amplifiers.

Although inductive boost converters can be highly efficient, improper selection of a converter type, operating frequency and/or external components can lead to an inefficient design. Therefore, making accurate efficiency calculations helps to identify the individual loss contributors and provides the insight necessary in designing an efficient boost converter.

To begin with, take a standard asynchronous boost converter. The simple approximation to efficiency can be made using a first-order model where the ideal duty cycle (D) = (V_OUT - V_IN)/V_OUT and the average inductor current, or input current (I_IN), I_IN = (I_OUT/1 - D) is used to estimate the dc losses in the NMOS switch, the Schottky diode and the inductor.

Efficiency then becomes:

where P_SWITCH = R_NMOS ´ D ´ (I_OUT/1 - D)², P_INDUCTOR = R_L ´ (I_OUT/1 - D)² and P_DIODE = R_D ´ I_OUT² + V_F ´ I_OUT.

This model makes for a rough estimate; however, the initial approximation for duty cycle ignores the circuit's internal losses and ends up underestimating the duty cycle as well as the input current. Essentially, the duty cycle must increase to overcome the circuit's internal losses. Consequently, the initial calculation for the duty cycle should have involved the component of efficiency or, more specifically:

This can be found by using the equation V_IN ´ I_IN ´ eff = V_OUT ´ I_OUT, substituting I_IN = (I_OUT/1 - D) and solving for D. Because of this, the first-order model's efficiency estimate will increasingly deviate from the actual efficiency as the power loss between the input and the output increases.

Accounting for this requires a model that computes the duty cycle based on the power-loss components and then uses this value to calculate the circuit's input current, again via the ratio I_IN = (I_OUT/1 - D).

In developing this model, consider the power balance in the boost regulator P_IN = P_LOSS + P_OUT. This states that the total input power is equal to the output power plus the power lost in each of the circuit's components. Again, using a typical asynchronous boost converter, the dc losses in the NFET switch, the diode and the inductor are used to generate a power-balance equation given by P_IN = P_{SWITCH +} P_DIODE + P_INDUCTOR + P_OUT.

Substituting I_IN = (I_OUT/1 - D), as was done before in the first-order model, leads to the modified power-balance equation:

Instead of using the ideal duty-cycle ratio D = (V_OUT - V_IN)/V_OUT, the power-balance equation is now used to solve directly for D. Multiplying by (1 - D)² and collecting the terms on one side gives a second-order polynomial for the duty cycle:

D² ´ (V_F ´ I_OUT + V_OUT ´ I_OUT + R_D ´ I_OUT²) + D ´ (R_N ´ I_OUT² + V_IN ´ I_OUT - 2 ´ V_F ´ I_OUT - 2 ´ V_OUT ´ I_OUT) + (R_L ´ I_OUT² + V_F ´ I_OUT + V_OUT ´ I_OUT - V_IN ´ I_OUT) = F(D)².

This becomes the second-order model that generates two solutions for D, one of which is correct (the first zero crossing of F(D) versus increasing D) and the other (the second crossing) is not. This can be solved using the quadratic formula.

Since only the dc losses are accounted for in this model, the efficiency estimate is only accurate when the converter operates in the continuous-conduction mode (CCM) with relatively small inductor current ripple and when the dc losses are much bigger than the switching losses. However, when this is not the case and the peak-peak inductor current ripple approaches (2 ´ I_OUT)/1 - D and/or switching losses begin to approach or surpass the dc conduction losses, this model begins to deviate from the actual efficiency, much the same way as the first-order model did.

To show the error in the first- and second-order models, consider an asynchronous boost converter such as National Semi's LM3528, which is designed to power two strings of white LEDs in an LCD backlight (Fig. 1). With the given circuit parameters, the measured efficiency is 83%.

Using the first-order model, the estimated duty cycle is:

The input current is calculated as:

The dc conduction losses in the NFET become:

D ´ I_IN² ´ R_N = 18 mW.

The diode losses become:

V_F ´ I_OUT + I_OUT² ´ R_D = 19.2 mW.

And the inductor loss becomes:

I_IN² ´ R_L = 15.6 mW.

This gives an approximated efficiency of:

The second-order estimate should yield a closer approximation to the actual efficiency since the circuit's internal losses are included in calculating the duty cycle. Taking the converter's parameters and using the quadratic formula to solve for D in the equation F(D²) gives a duty cycle of 0.825. This results in a slightly lower efficiency:

However, this efficiency is still quite a ways off from the actual value.

Switching Losses

Where does the problem lie? For boost converters such as white LED drivers that operate with such low output currents and high duty cycles, the switching losses are no longer trivial compared to the circuit's conduction losses. The switching-loss components must be included in the second-order power-balance equation to give a more accurate estimate of the duty cycle and a closer calculation of circuit efficiency.

To start with, the primary switching-power loss components in an asynchronous boost converter include the power due to the MOSFET cross conduction (P_CC), which is the overlap between the current and voltage during the switch turn-on and turn-off, the charging of the Schottky diode's capacitance with each switching cycle (P_CD), and the charging of the NFET switch's drain-to-source capacitance each switching cycle (P_CDS).

Adding these to the power-balance equation gives a more complicated (but accurate) equation of the duty cycle. The new second-order power-balance equation becomes:

This results in a modified second-order equation for a duty cycle of:

Using C_DS equals 40 pF, C_D equals 20 pF and t_RISE equals t_FALL equals 8 ns results in an estimated duty cycle of 83.8% for the LM3528. This results in a calculated efficiency of 85.5%, which is much closer to the measured value.

Higher-Order Model

Until now, the duty-cycle calculations assumed no ripple current, which isn't a problem because an average inductor current is used instead of root-mean-square (rms) inductor current. And assuming the converter operates in the CCM only changes the previous answer a slight amount. However, with boost circuits operating at such low-output power levels, it is likely that a large portion of the load current will cause the converter to operate in a discontinuous conduction mode (DCM).

Unfortunately, the previous calculations only applied to the CCM. If the designer wants to model the DCM efficiency, then the ripple current is no longer trivial. Furthermore, to calculate efficiency over the entire load-current range, ignoring the ripple current in the CCM and then including it in the DCM would lead to a discontinuity in efficiency as the load current transitions through the modes.

The solution is to include the ripple current in the CCM duty-cycle equation and also solve for the duty cycle using a separate equation for the DCM. The DCM equation is developed using a power-balance equation in much the same way as for the CCM case.

As a starting point, the rms value of a triangle waveform, which is the true inductor current, is given by:

I_LDC is the dc or average value of the inductor current, which is I_OUT/1 - D for the CCM and zero for the DCM. ΔI_L is the peak-to-peak inductor current ripple and is given by (ΔI_L = V_IN ´ D/(f_SW ´ L)) for both the CCM and the DCM. Finally, d is the portion of the switching period that the rms current is conducting.

For example, d = D for the components conducting during the switch-on time in both the CCM and the DCM; d = (1 - D) for the components conducting during the off time in the CCM and d = (2 ´ I_OUT)/ ΔI_L for the components conducting during the off time in the DCM; and lastly, d = 1 for the components conducting during both portions of the period in the CCM and d = D + (2 ´ I_OUT)/ ΔI_L for the components conducting during the first two portions of the period in the DCM.

Adding the ripple component to the F(D²) equation adds a third-, fourth- and fifth-order term for the resistive power-loss components. On the other hand, the DCM equation becomes a third-order polynomial. To avoid the complexity of drawing out these equations, the table categorizes the power-loss components in the asynchronous boost converter with the factored D terms to the right. In the table, the first column lists the CCM components and the second column lists the DCM components.

Each term in the CCM column is normalized to I_OUT (i.e., it is divided by (1 - D)² to eliminate the (1 - D)² term in the denominator). The I_AC term is the inductor current slope over the entire switching period (or the inductor current ripple divided by D). Collecting the terms of the power-loss components in the CCM column results in the fifth-order polynomial, F_CCM (D⁵) = a ´ D⁵ + b ´ D⁴ + c ´ D³ + d ´ D² + e ´ D¹ + f ´ D⁰, and collecting the terms of the power-loss components in the DCM column gives a third-order polynomial, F_DCM (D³) = g ´ D³ + h ´ D² + j ´ D¹ + k ´ D⁰, where the a through k coeffecients are functions of the circuit parameters V_IN, V_OUT, I_OUT, R_N, R_L, etc.

This higher-order model using both the F_CCM(D⁵) and F_DCM(D³) equations has no simple solution like the F(D2) equation. Fortunately, as with F(D²), the useful solutions to the fifth- and third-order polynomials are those occurring at the first crossing of zero with increasing D.

Finding this solution is possible, using a spreadsheet like Excel, by setting F(D⁵) and F(D³) to zero and plotting F(D) versus D and varying D from zero to one. Alternatively, implementing the functions F_CCM(D⁵) and F_DCM(D³) in C and using a “while” loop to test for the first F(D) = 0 crossing versus increasing D works, also.

Comparing the calculated values with measured values using the higher-order model requires that a converter be used that operates in either the CCM or the DCM. Unfortunately, the LM3528 operates in a pulse-skip mode to improve efficiency at light loads. This would require a third equation to model the converter in this mode. Additionally, using a white LED driver adds an extra layer of complexity in the calculations since the LED voltage changes with I_OUT.

To remedy this, the LM27313 standard asynchronous boost converter will be used to compare the calculated versus measured results of the efficiency estimations (Fig. 2). This converter operates in either the CCM or the DCM over the entire load current range, thus providing a more direct comparison with the developed higher-order model.

Fig. 3 and Fig. 4 use the equations developed so far for the first-, second- and higher-order models to calculate D and solve for efficiency versus output current. The LM27313's output voltage is held at 19 V over the entire load current range of 0 mA to 40 mA (Fig. 2).

Fig. 3 compares the first-order model, the second-order model, both with and without switching losses, the higher-order model and the measured efficiency. Fig. 4 also compares the measured efficiency with the calculated efficiency using the higher-order model as previously described, and the higher-order model that is slightly modified to account for changes in C_D and C_DS capacitive energy losses at very light loads.

The first-order model again uses the ideal duty-cycle ratio and calculates efficiency at each I_OUT. Both second-order models (for dc losses only) and second-order switching losses use the F(D²) equation and solve for D at each I_OUT using the quadratic formula. The higher-order model uses C code and iterates through the F_CCM(D⁵) equation by varying D between 0 and 1 while testing for the first zero crossing. At the end of each F_CCM(D⁵) iteration, a comparison is done between the calculated inductor current ripple and the average inductor current to determine when:

When this happens, the converter is assumed to be in the DCM, and the F_DCM(D³) equation is then iterated to calculate D. This is done at each I_OUT to generate the efficiency graph.

As would be expected, the first- and second-order (dc only) models show a lot of variation between the calculated and actual efficiency. The second-order model, which includes switching losses, is the closest at low currents while the higher-order model is closer at high currents, but tends to deviate at low currents when the device operates further into the DCM.

This can be explained by understanding how the boost-circuit capacitances charge and discharge each switching cycle as the boost converter transitions from the CCM to the DCM. When the converter is operating fully in the CCM, the drain-to-source and diode capacitances charge and discharge from zero to V_OUT, each cycle causing a power loss of:

As the converter transitions from the CCM to the DCM (i.e., the load current decreases), the inductor current slope will hit zero before the end of the switching period. If the inductor current hits zero well before the end of the switching period, the inductor current will begin to go negative, causing the energy in the switching node capacitances to return back to V_IN. As the load current is further reduced, the dead time increases and a damped ringing develops between the switching node capacitances and the inductor. Eventually this voltage ringing will decay to V_IN.

The result is that as the converter transitions more and more into the DCM, the switching node capacitances will give a lot of their energy back to the input and essentially have to charge up to a smaller and smaller voltage. At the extreme minimum current, when the switching node has discharged down to V_IN before the start of a new switching period, the drain-to-source and diode capacitance power loss becomes closer to:

If the third-order DCM equation is made to reflect this, then the efficiency versus load current becomes closer to the actual efficiency at light currents (Fig. 4). The discontinuity in the modified higher-order plot occurs at the CCM/DCM boundary where the C_DS and C_D capacitance voltage begins shifting from V_OUT down to V_IN.

Another source of error that was left out of the duty-cycle calculations is that due to inductor switching losses (core loss and eddy currents). This would tend to decrease the efficiency even further when the converter operates in the DCM due to the large current ripple. Unfortunately, inductor ac switching-loss values are not commonly given, so they were not used in these examples.