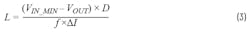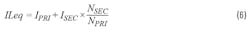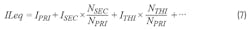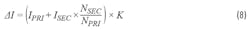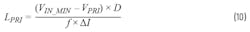Members can download this article in PDF format.
What you'll learn:
- Basics of an isolated buck converter.
- Key specifications to consider in transformer selection.
- Steps involved in choosing the right transformer.
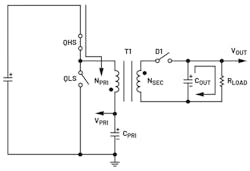
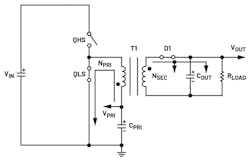
An isolated buck topology (Fig. 1) is similar to a generic buck converter. By replacing the inductor in a buck circuit using a transformer, we can get an isolated buck converter. The transformer’s secondary side has an independent ground.
During on-time, the high-side switch (QHS) is on and the low-side switch (QLS) is off. The transformer’s magnetizing inductance (LPRI) is charged up. The arrows in Figure 2 show the current flow direction—the primary current increases linearly. The current ramping slope depends on (VIN – VPRI) and LPRI. The secondary-side diode, D1, is reverse-biased during this time interval and loads current flow from COUT to load.
During off-time, QHS is off and QLS is on and the primary inductor is discharged (Fig. 3). The primary current flows from QLS to ground, D1 is forward-biased, and the secondary current flows from the secondary-side coil to COUT and to load. COUT is charged up in this time period. (Turning off QHS and turning on QLS can’t change current direction; it can only change the current slope. The positive current decreases until 0 A; then the negative current increases.)
Which Specifications Will Influence the Transformer?
When designing a converter, some specifications should be declared and cleared:
- Input voltage range
- Output voltage
- Maximum duty cycle
- Switch frequency
- Output voltage ripple
- Output current
- Output power
It will determine the component to be used, especially when choosing a transformer.
Maximum duty cycle (D) is usually assigned in the range of 0.4 to 0.6. The minimum input voltage (VIN_MIN) and maximum duty cycle will determine the primary output voltage (VPRI). Then, the primary output voltage (VPRI) and secondary output voltage (VOUT) will determine the transformer turns ratio.
Output current (IOUT) and output power (POUT) are key parameters that influence transformer selection. Output current determines the thickness of the copper wire, while output power determines which transformer bobbin should be used. The permeability of the bobbin shows how much energy it can store and how much power it can put out.
Generally, the DC output current multiplied by a coefficient is assigned to the inductor’s (transformer’s) ripple current. Duty cycle and switch frequency are used to calculate TON time, while VIN, VPRI, and ripple current determine the primary inductance. The assigned coefficient must not be too large or too small since a large coefficient can lead to a large ripple current.
A large ripple current may reach half of the H-bridge current limit and damage the MOSFET. This will lead to a large ripple voltage on the output capacitor due to its ESR and ESL. On the contrary, when an extremely small ripple current is needed, we need to use a high-inductance-value inductor (transformer). If the coil has many turns, this will require a bulky bobbin. The large inductance will limit loop bandwidth and reduce the dynamic response index.
Choosing a Transformer
Energy is transmitted to secondary coil only in TOFF time. The turns ratio can be determined by Equation 1:
where VD is the secondary diode forward-bias voltage. For VPRI, we usually assign a maximum duty cycle in the range of 0.4 to 0.6. The VPRI can be calculated using Equation 2:
where D is the maximum duty cycle and VIN_MIN is the minimum input voltage. From Equation 2, we can calculate the turns ratio.
In a non-isolated buck converter, the ripple current is the same on both sides of the inductor. We can easily calculate the inductance required using Equation 3:
where f is the switching frequency and ΔI is the ripple current. As discussed previously, ripple current equals the DC output current multiplied by a coefficient:
where K is the coefficient. But in an isolated buck-converter topology, there’s a transformer and not an inductor. How do we deal with it when the component is a transformer rather than an inductor? As we know, the current ratio equals the inverse of the turns ratio:
where IPRITOFF is the secondary current that’s converted to a primary current in TOFF time. We should add a transformer’s two-coil current as an equivalent inductor current:
where ILeq is the equivalent inductor current. If the transformer has three more windings, then:
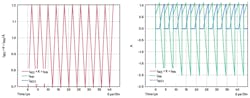
Is this correct? Let’s see a simulation result based on the MAX17682. Figure 4 shows a MAX17682 circuit, which was drawn in EE-Sim OASIS, powered by SIMetrix/SIMPLIS. Current probes, labeled IPRI and ISEC1, have been placed at both sides of the transformer.
Figure 5 shows a transient simulation result from the two probes. The two current waveforms were added utilizing Equation 6.
The added current results (red) in a triangle wave and behaves just like the inductor in a non-isolated buck converter. Therefore, the transformer’s primary ΔI can be easily calculated:
Usually, we assign a load ripple current that is 0.2 times the DC output current. So, K can be assigned to 0.2 × NSEC/NPRI. At the same time, the primary peak current should be designed less than the switch current limitation, where IPK is:
Then the transformer’s primary inductance can be easily calculated:
By using the turns ratio, primary inductance, output power, output current, and isolation voltage, we can decide which inductor will be used or designed.
Why a Simplified Equation Can Work
Let’s see how we can better understand and apply the equation shown in the MAX17682 datasheet (Fig. 6).
According to the previous discussion, Equation 10 can be rewritten to follow Equation 11 for TOFF time:
Assuming D is 0.6, if and only if ΔI were 0.4 A, the polynomial (1 – D) and ΔI can be reduced. Then Equation 11 and the equation from Figure 6 are the same. The equation in the datasheet already selects the primary ripple current. If we assign D as 0.6, the primary ripple current is 0.4 A. In quantity, TOFF duty cycle equals the primary ripple current:
Conclusion
By using the simplified equation shown in Figure 6, the user ensures a faster design with a primary ripple current that equals the TOFF duty cycle. If you want to modify primary ripple current or use another parameter, you can follow this tutorial.