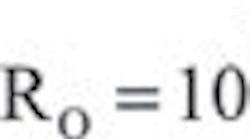It may come as a surprise to some that a control loop’s Bode plot does not always depict the loop stability and that the output impedance measurement, obtained non-invasively, always does. Challengers of the non-invasive phase margin measurement approach believe that the method is not always an accurate representation of loop phase margin. While this can be true for transfer functions that are more than first order, the Bode plot does not always accurately depict the control loop stability in these cases either, while the non-invasive output impedance measurement does. It is important to note, however, that the impedance must be measured at the feedback points, since downstream filters can impact the results. This is not to say that the downstream impedance is unimportant, it certainly is for Power Distribution Network (PDN) evaluations, however; the filters (and trace impedances) can mask the loop stability.
Case study of a five output winding flyback converter
The phase margin and gain margin do not necessarily provide an accurate assessment of the control loop stability. Let’s look at one case study of a five output winding flyback converter, where the Bode plot leads to an incorrect conclusion of stability. The Bode plot for the converter, in Fig. 1, indicates a bandwidth of 650Hz and a phase margin of 50 degrees. The small signal step load, Fig. 2, and the output impedance measurement, Fig. 3, indicate otherwise. The small signal step load shows ringing at a frequency of 850Hz, which is higher than the 650 Hz bandwidth. The small signal output impedance measurement indicates an impedance peak coinciding with the 850 Hz ringing frequency seen in the small signal step load response. Both the small signal step load and the non-invasive output impedance measurement predict a phase margin of approximately 20 degrees, which is significantly worse than the 50 degree phase margin indicated by the Bode plot. The Bode plot includes markers for the gain and phase at both the 658Hz crossover frequency and also at the ringing frequency of 850Hz.
Why are the various measurements in disagreement? In fact, maybe they are not; it’s possible the tests are simply measuring different performance aspects. The Bode plot reports the phase margin at the gain crossover frequency and the gain margin at the phase crossover frequency. These two margins do not necessarily provide a complete assessment of the control loop’s stability. This revelation is not new and is supported by the seldom- used Nichols chart. The Nichols chart is used to determine the peak response (most unstable point) from an open loop transfer function plot, as well as the crossover frequency, phase margin and gain margin. The peak response does not necessarily coincide with the gain crossover frequency. This can also be evident when using Nyquist plots and RF gain circles.
Determining the stability of the control loop
The goals of the small signal step load (indirectly) and output impedance measurements (directly) are to determine the stability of the control loop. These measurements are easily acquired using the Picotest J2111A Current Injector and a vector network analyzer (VNA). The J2111A is minimally invasive, presenting a significantly lower capacitance load compared with normal electronic loads while enabling load transition edge speeds as fast as 20nSec and repetition rates above 10MHz.
The output impedance plot is captured, in this case, using an OMICRON-Lab Bode 100 VNA along with the J2111A. Looking at a Nyquist plot representation of the control loop in Fig. 4 reveals why the stability is worse at a frequency other than the crossover frequency.
Fig. 4 shows that the distance from the open loop frequency response is closer to the singular unstable point (1, 0) at (0.598, 0.232) than the unity gain circle crossover point, with an associated phase lower than indicated by the phase margin.
The closest distance from (1, 0) occurs at 850Hz, which is the frequency at which the ringing is seen in the small signal step load response and also coincides with the peaking seen in the output impedance measurement. This distance measurement is also similar to the stability circles used by RF engineers to determine the stable regions of RF amplifiers.
The second case study utilizes a simple op-amp circuit. The Bode plot, output impedance, and small signal step load are all simulated,as shown in Fig. 5.
The Bode plot shown above in Fig. 6 has a phase margin of 46 degrees at a crossover frequency of 3.92MHz. The minimum distance from (1,0) occurs at 5.50MHz with a phase of 34 degrees. The minimum distance from (1, 0) occurs at 5.50MHz with a phase of 34 degrees as shown in Fig. 7.
The output impedance plot in Fig. 8 shows that there is a peak at 5.5MHz and not at the gain crossover frequency of 3.92MHz. The resonant peak can be converted to a characteristic resistance which along with the effective inductance and capacitance can determine the Q. Ro peak:
Effective inductance:
Effective capacitance:
The equation to convert Q into phase margin can be found in Reference 1.
The small signal step load response in Fig. 9 shows that the ringing frequency is 4.44MHz with a Q more indicative of 35 degrees rather than 45 degrees.
While the Bode plot can be used to determine the phase margin and gain margin of a control loop, it is not always the best indicator of the overall stability. The two case studies shown here both result in acceptable phase margins, while the small signal step load and output impedance measurements indicate performance that is worse than expected based on the measured phase margin and may not be acceptable for some applications.
The least stable point does not necessarily coincide with the 0dB gain crossover frequency as the open loop transfer function can be closer to the unstable point (1, 0) at other frequencies and gains. This can be seen in the Nyquist plot, Nichols chart and also using gain circles. The significant outcome is that while the Bode plot, small signal output impedance and small signal step load response are generally in agreement this is not always the case.
An additional consideration is that that the interest in assessing stability is not an interest in the phase margin as a number, but of the effect it has on the closed loop performance, as seen in PSRR, reverse transfer, step load and output impedance. These are better assessed through output impedance, small signal step load response, or PSRR testing or analysis.
References
- Erickson, Robert W. and Dragan Maksimovic. Fundamentals of Power Electronics. Second Edition. Springer, 2001.
- Åström, Karl Johan and Murray, Richard M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, 2008.
- Doyle, Francis and Tannenbaum. Feedback Control Theory. Macmillan Coll Div, 1992.
Related Articles:
Understanding the Right-Half-Plane Zero - Part 1
Understanding the Right-Half-Plane Zero
Compensating the RHPZ in a CCM Boost Converter: the Analytical Way
Compensating the RHPZ in a CCM Boost Converter: Using a Simulator
About the Author
Steve Sandler
Steve Sandler is the founder and chief engineer of AEi Systems LLC and the president of Picotest. At Picotest he is responsible for signal injector product development, as well as the overall operation of the test equipment company.