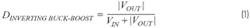How to Leverage the Inverting Buck-Boost in High-Voltage Apps

This article is part of the TechXchange: Power Supply Design

Members can download this article in PDF format.

What you'll learn:

What are the three main non-isolated topologies?
What to consider when designing high-voltage apps using the inverting buck-boost.
Other design considerations when dealing with even higher voltages.

A variety of topologies can be considered for applications that require thegeneration of a negative voltage rail, as illustrated in the article “The Art of Generating Negative Voltages.”¹ However, if the absolute voltage at the inputand/or output can exceed 24 V and the required output current may reach a fewamperes,thechargepumpandthenegativeLDOregulatoraretobediscardeddueto their low current capability. Also, the size of their magnetic componentscausestheflybackandtheĆukconvertersolutionstobecomequitecumbersome.As a result, under such conditions, the inverting buck-boost provides the bestcompromise between high efficiency and small form factor.

To reap these benefits, though, the operation of the inverting buck-boost topology under high-voltage conditions must be fully understood. Before diving into suchdetails, we will begin with a brief review of the inverting buck-boost topology.Then,wewillcomparethecriticalcurrentpathsoftheinvertingbuck-boost,buck,and boost topologies.

TheThreeBasicNon-Isolated Topologies

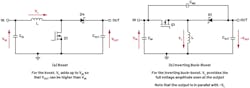
The inverting buck-boost belongs to the grouping of three basic non-isolated switching topologies. These topologies all consist of a control transistor (usually a MOSFET), a diode (either a Schottky diode or an active diode—the synchronous MOSFET), and a power inductorastheenergy-storageelement.Thecommonconnectionbetweenthosethree elements is referred to as the switching node. The positioning of the power inductor withregardtotheswitchingnodedeterminesthetopology.

If the coil is located between the switching node and the output, we obtain thedc-dc buck converter, which we simply call buck in the rest of this article.Alternatively, positioning the coil between the input and switching node createsthe dc-dc boost converter, referred to as boost here. Finally, the dc-dcinvertingbuck-boostconsistsofplacingthecoilbetweentheswitchingnodeandground(GND).

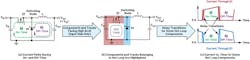
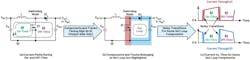
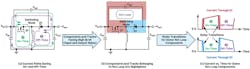
Duringeachswitchingperiodandevenincontinuousconductionmode(CCM),allthreetopologiesincludecomponentsandPCBtracesthatarefacingfastchangesincurrent,leadingtothenoisytransitionshighlightedinFigures 1c, 2c, and 3c. By keeping the hot-loop small, the electromagnetic interference (EMI)radiated by the circuit can be reduced.

1.Componentsandtracks belongingtothehot loop—buckconverteroperatingin CCM.

2.Componentsandtracks belongingtothehot loop—boostconverteroperatingin CCM.

3.Componentsandtracksbelongingtothehotloop—invertingbuck-boostoperatingin CCM.

At this stage, it’s worth mentioning thatthe hot loop isn’t necessarily a physical loop through which the current circulates.Indeed,fortherespectiveloopshighlightedinFigures 1-3,thesharpcurrenttransitionsdon’toccurinthesamedirectionforthecomponents and tracks highlighted in red and blue that form the hot loop.

For the inverting buck-boost operating in CCM (Fig. 3), the hotloopconsistsofC_INC,Q1,andD1.Comparedwiththehotloopofthebuckandboosttopologies,thehotloopoftheinvertingbuck-boostcontainscomponentslocatedbothontheinputandoutputsides.Amongthesecomponents,thereverserecoveryofthediode(orbodydiodeifusingasynchronousMOSFET)whenthecontrolMOSFETturns on generates the highest di/dt and EMI.

Since a thorough layout conceptis needed to contain the radiated EMI from these two sides, the last thing youwantistocreateadditionalradiatedEMIthroughexcessivecoilcurrentripplebyunderestimatingtherequiredinductanceoftheinvertingbuck-boostunderhighinputand/oroutputvoltageconditions.Thisriskexistsforengineerswhorelyontheir familiarity with the boost topology to size the inductance of their invertingbuck-boost circuit, as we now see by comparing both topologies.

DesignConsiderationsofInvertingBuck-Boost with High Voltages

Both the boost and the inverting buck-boost can generate an absolute output voltage whose amplitude is higher than the input voltage. There are, however, relevantdifferencesbetweenbothtopologiesthatcanbehighlightedwiththehelpoftheirrespectivedutycyclesinCCM,providedinEquation1andEquation2.Pleasenotethatthesearefirst-orderapproximationsthat don'tconsidereffectssuchasthevoltage drops through Schottky diodes and power MOSFETs.

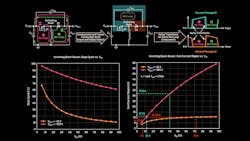
The first-order approximation for the variation of these duty cycles vs. |V_OUT|, andwith V_IN = 12 V, is plotted on the left side of Figure 4. Moreover, assuming in bothcasesaswitchingfrequency(f_SW)of1MHzandaninductanceof1µHforthepowercoil,thevariationofthecoilcurrentripplevs.V_OUTwasobtainedontherightsideof Figure 4.

4.Dutycycleandcoilcurrentripplevs.|V_OUT|atV_IN=12Vforinvertingbuck-boostandboost.

WeobserveinFigure4thatthedutycycleofaninvertingbuck-boostwillexceed50%fromamuchlower|V_OUT|thantheboost:12Vand24V,respectively.Itcanbeunderstood by referring to Figure 5.

5. Impact of the coilpositioning on the obtained output voltage.

In the case of the boost, the inductor is in the path between input and output.Therefore, the voltage through the power inductor (V_L) adds up to V_IN to providetherequiredV_OUT.However,fortheinvertingbuck-boost,V_Listhesolecontributorto the achieved output voltage. On that occasion, the power inductor must provide much more energy to the output, which explains why the duty cycle alreadyreaches 50% for a much lower |V_OUT|.

We can reformulate this observation by stating that, as the ratio |V_OUT|/V_INdecreases, the duty cycle drops at a much slower rate for the inverting buck-boost than fortheboost.Thisisanimportantfacttoconsiderduringdesign,anditsimpactcanbebetterunderstoodbyreferringtoFigure6,wherethefirst-orderapproximationof the duty cycle and coil current ripple are redrawn, but this time vs. V_IN.

6.Dutycycleandcoilcurrentripplevs.V_INat|V_OUT|=48Vforinvertingbuck-boostandboost.

AsdemonstratedinFigure6,thecoilcurrentripple(ΔI_L)isproportionaltoV_IN and D. In the case of the boost, as V_IN becomes higher than half of V_OUT, thedutycycledecreasesfasterthanV_INincreases,goingfrom50%atV_IN=24Vtoaquarter of this value at V_IN = 42 V for the blue curve in the left graph of Figure 6.Consequently, ΔI_L decreases quickly for V_IN above 24 V for the boost on the rightgraph of Figure 6.

But, for the inverting buck-boost, we previously saw in Figure 4 that Ddecreases very slowly when |V_OUT|/V_IN decreases. In other words, when V_INincreasesforafixed|V_OUT|.Thiscanbeseenforthegreencurveontheleftgraphof Figure 6, where the duty cycle loses only 25% when V_IN increases by 62.5%from48to78V.SincethedecreaseinDdoesn’tcompensatefortheincreasein V_IN, the coil current ripple increases significantly with V_IN, as illustrated by thegreen curve in the right graph of Figure 6.

Overall, the higher coil current ripple potentially faced under high-voltageconditions by the inverting buck-boost compared with the boost explains whytheformertopologyrequireshighercoilvaluesifoperatingatthesamef_SW.Let’susethisknowledgeinaconcretecasewiththehelpofFigure7,whichalso isbased on first-order approximations.

7.Dutycycleandcoilcurrentripplevs.V_INatV_OUT=–12Vand–150Vforinvertingbuck-boost.

Application with Wide Input Voltage Range and High Output Current

Let’s consider an application with V_IN = 7 to 72 V and V_OUT = –12 V at 5 A. Giventhehighoutputcurrent,weoptforasynchronouscontroller(LTC3896)toachievehighefficiency.

Selectingthe Inductance

WhenoperatingtheLTC3896inCCM,it’srecommendedtokeepΔI_Lbetween30%and70%ofI_OUT,MAX,whichis5Aforourexample.Consequently,wewanttodesignforΔI_Lbetween1.5and3.5Aoverourwholeinputvoltagerange.

Moreover, staying within this recommended range between 30% and 70% of I_OUT,MAX means that wecan only afford a ratio of up to 2.33—that is, 70% divided by 30%—between thehighestandlowestcurrentrippleoverourinput-voltagerange.Thisisn’tatrivialtaskforatopologysuchastheinvertingbuck-boost,whereΔI_Lvariessignificantlywith V_IN, as previously observed.

Referring to Figure 7, when using f_SW = 1 MHz and L = 1 µH, the coil current ripplewouldvarybetween4.42and10.29A,whichisfartoomuch.TopositionthelowestΔI_Ltoourrecommendedlowerlimitof1.5Aor30%ofI_OUT,MAX,weneedtoreducetheexistingvalueof4.42Abyafactorofthree.Thiscanbeachievedbysettingf_SWto300kHzwitha47.5-kΩresistorattheFREQpinandselectinga10-µHinductance.Indeed,thisscales downΔI_Lby(1 µH×1 MHz)/(300kHz×10 µH)=1/3.

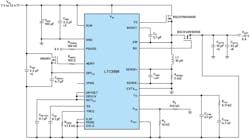
Thankstothisscaling,thecoilcurrentripple, or ΔI_L,shouldnowvarybetweenabout 1.5 and 3.4 A (between 30% and 68% of I_OUT,MAX) over the whole input voltagerange, which is just within the recommended range. We obtain the circuit providedon the last page of the LTC3896 datasheet, which is reproduced in Figure 8.

8.LTC3896circuitwithV_IN=7to72V,V_OUT-=–12V,andf_SW=300 kHz.

ValidatingOurInductanceSelectionwithLTspice

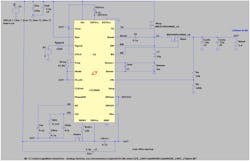
Regarding the coil current ripple, more accurate values can be obtained by simulating the same LTC3896 circuit with LTspice, as demonstrated in Figure9.

9.LTC3896circuitsimulatedwithLTspice.

In Figure10, ΔI_L equalsabout1.45Aand3.5A atV_IN=7Vand72V, respectively, whichisconsistent with the first-order approximation values previously extracted with the help ofFigure7andthescalingofthef_SWandL.Pleasenotethatthecoilcurrentprobedin Figure 10 is considered positive when flowing toward R_SENSE.

10.MeasuringΔI_LatV_IN=7and72VandextractingthepeakcoilcurrentwiththepreviousLTspicecircuit.

An additional benefit of the LTspice simulation is to determine the peak coil current facedduringoperation,whichisobtainedatthelowestinputvoltageof7V.AsseeninFigure10,ourapplicationwillfaceapeakcoilcurrentcloseto15.4A.Byknowingthisvalue,apowerinductorwithahighenoughcurrentratingcanbeselected.

DesigningwithEvenHigherOutput Voltages

Returning to Figure7, current ripple values also were provided for a hypothetical casewithaV_INrangefrom12to40VandaV_OUTequalto–150V.

The first remark is that the current ripple is getting significantly higher for higher V_OUT whenkeepingthesamef_SWandL.SuchhighΔI_Lareoftenunacceptable. Therefore,wewouldhavetoapplyahigherscalingdownfactorcomparedwiththepreviousexample, which means a higher inductance for the same f_SW.

ThesecondremarkreferstothevariationofΔI_Loverthewholeinputvoltage range.ForthepreviousexamplewithV_OUT=–12V,ΔI_Lwasonlyincreasingbyabout 2.33 from lowest to highest ripple, with the input voltage increasing more thantenfold.ForthepresentcasewithV_OUT=–150V,ΔI_Lalreadyincreasesby2.85fromlowesttohighestcurrentripple—andthisdespitetheinputvoltageonlyincreasingby a factor 3.33 from 12 to 40 V.

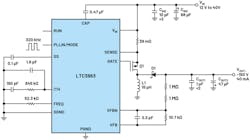
Luckily, such challenges only exist in CCM. When in discontinuous conductionmode (DCM), limitations such as 30% to 70% of I_OUT(MAX) no longer apply. As it is, it wouldbe too strenuous to convert V_IN = 12 V to V_OUT = –150 V at I_OUT(MAX)= 5 A in asingle step. In any case, when such voltage conversions are required, the output-current requirement is generally low, meaning that we operate in DCM. This is,for example, the situation for the circuit on the last page of the LTC3863 datasheet,reproduced in Figure 11.

11.AnLTC3863circuitwithV_IN=12Vto40V,V_OUT-=–150V,andf_SW=320 kHz.

Due to the low dc currents, using a nonsynchronous controller such as the LTC3863 was good enough to provide an acceptable efficiency under these conditions. In the caseofthisLTC3863designinDCM,theLTC3863circuitprovidedwithLTspiceisanice tool to optimize the coil selection.

Conclusion

The hot loop of the inverting buck-boost topology includes components located on both the input and output sides, making its layout more difficult to implement than the buck and the boost topology.

Although there are some analogies to the boost, the inverting buck-boost faces much more current ripple under similar application conditions because its coil constitutes the only source of energy to the output (if we ignore the output capacitance).

For inverting buck-boost applications with high input and/or output voltages, the coil current ripple is potentially even higher. To contain it, higher inductance values are usedcomparedwiththeboosttopology.Apracticalexamplewasusedtodemonstrate how to quickly scale the inductance based on the application conditions.

Read more articles in the TechXchange: Power Supply Design