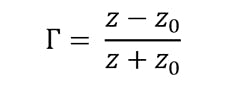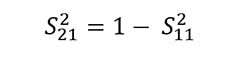An Introduction to the VNA and Vector Network Analysis
This article appeared in Microwaves & RF and has been published here with permission.
Members can download this article in PDF format.
What you’ll learn:
- What does a VNA measure?
- What can one do with the measured data?
- What devices are measured with a VNA?
Most design engineers are familiar with tools of the trade such as voltmeters, oscilloscopes, signal generators, and spectrum analyzers. Some may not have had the opportunity to use a vector network analyzer (VNA). It’s the intent of this article to introduce VNA measurement and present a few typical applications.
Why is a VNA Useful?
Transmission lines can support RF propagation in either direction. Signals traveling along a transmission line may encounter localized impairments that aren’t precisely 50 Ω, such as connectors or transitions from coaxial to planar media (other impedances such as 75 Ω are common, but for the purposes of this explanation we will use 50 Ω). Each impairment generates a reflection that travels back toward the source along the transmission line.
A 50-Ω load on the end of a 50-Ω transmission line absorbs all signal energy and reflects nothing. Any load other than 50 Ω will generate some amount of reflection. The farther the load is from 50 Ω, the greater the reflection. A short and an open circuit reflect the entire signal back to the source. To characterize reflections, we introduce the reflection coefficient (Γ):
where z0 is the characteristic impedance of the source and transmission line and z is the complex impedance of the load.
If z is 0—a short—then Γ = −1, or a complete reflection that’s 180 degrees out of phase with the incident signal. If z is infinite—an open—then Γ = 1, or a complete reflection in phase with the incident signal. If z = z0—a 50-Ω load—then Γ = 0, which means no reflection at all.
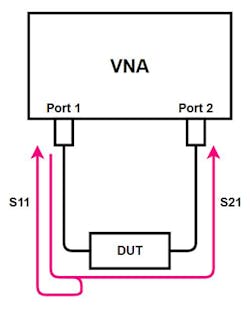
A VNA can separate and measure incident and reflected signals, and thus directly determine reflection coefficients. Figure 1 depicts a VNA measurement. The incident signal exits the VNA from Port 1 and arrives at the input to the device under test (DUT). At that interface, there may be some reflection that returns to Port 1. The remainder of the signal passes through the DUT and enters Port 2 of the VNA. Two receivers at Port 1 measure both incident and reflected waves and a receiver at Port 2 measures the wave entering there.
We call the ratio of the incident wave to the reflected wave—the reflection coefficient—S11. The ratio of the signal entering Port 2 to the incident signal leaving Port 1 is called S21. Figure 1 shows both.
In the real world, there would be reflections from within the DUT and another reflection at the output connector, but they’re not shown to keep the diagram simple.
There are only a few possibilities for what can happen to the incident signal:
- It can be reflected back to the source in one or more places.
- It can be dissipated as heat within the DUT.
- It can be radiated away by the DUT.
- It can pass through the DUT and make its way to Port 2.
If the signal isn’t dissipated or radiated, then a direct relationship exists between S21 and S11. That is:
This is simply a conservation of energy statement. Signals that aren’t being reflected must pass through the DUT.
What Does a VNA Measurement Look Like?
In the actual measurement shown below, a 4-GHz bandpass filter is connected to an SC5090, a 9-GHz 2-port analyzer (Fig. 2).
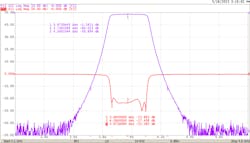
The purple trace in Figure 3 shows S21 in log magnitude format. This is the signal that passes through the filter from Port 1 to Port 2. Markers 2 and 3 indicate the points at which the filter attenuation is 60 dB. Marker 1 is set to the middle of the filter, where most of the signal is passing with little attenuation.
In this chart, the dB scale on the left side is relevant to the red S11 trace, and the zero for S21 is at the top of the screen. The markers show actual values.
The red trace shows S11, which is the reflection from the filter. In places where the filter isn’t passing the signal, it’s being completely reflected. In this case, 0 dB is equal to a linear “1,” or complete reflection. In the places that have almost no reflection—where S11 is less than −20 dB—the signal is passing through the filter with very little loss.
When speaking of filters, the measurement through the filter—the insertion loss—is the S21 reading within the passband and the return loss is the S11 measurement in the passband. Here, the insertion loss is 1.2 dB in the middle of the passband, and the return loss is better than 20 dB. Both numbers are traditionally stated as positive values, even though the S-parameters themselves are negative.
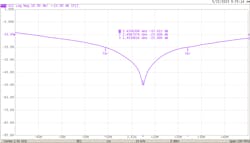
Figure 4 shows measurements being taken on a Wi-Fi antenna. This antenna receives and transmits in the 2.4-GHz band. A one-port measurement of the antenna reveals a sharp dip in S11 at 2.42 GHz and reasonably low values across the measurement range (Fig. 5).
Because S11 shows very little reflection—or high return loss—across the Wi-Fi band, the stimulus signal from the VNA must be efficiently radiating away. This antenna is therefore functioning properly.
The Touchstone Matrix
S11 represents the ratio of the reflection back to Port 1 to the signal emitted by Port 1, and S21 is the ratio of the signal measured at Port 2 to the signal emitted by Port 1. Similarly, S22 is the ratio of the signal reflected back to Port 2 to the signal emitted by Port 2, and S12 is the ratio of the signal measured at Port 1 to the signal emitted by Port 2. These last two might be called reverse measurements, as the signal is being emitted by Port 2 instead of Port 1.
If all four S-parameters are known over frequency for a linear two-port DUT, then this represents a complete characterization of the device. The S-parameters, saved in Touchstone format, may be used in a linear simulator to study how the DUT will behave with various RF excitations and loads.
Conclusion
The VNA measures the RF properties of a DUT by emitting an RF voltage wave and subsequently measures how much of it is reflected and how much passes through the DUT for a two-port measurement. For a one-port measurement, it simply measures the reflected wave. A low reflection means that the signal enters the DUT and very little returns.
Measurements such as that may be performed to determine the function and suitability of an unknown device or to create a Touchstone file for use in linear simulation. This makes the VNA a very powerful tool for the RF engineer.
Copper Mountain Technologies produces a wide range of VNAs with output frequencies from 1.3 to 330 GHz. Visit www.coppermountaintech.com for product information and educational articles and videos on vector network analysis.
About the Author
Brian Walker
Senior RF Design Engineer, Copper Mountain Technologies
At Copper Mountain Technologies, Brian Walker is the Senior RF Engineer helping customers to resolve technical issues and working to develop new solutions for applications of VNAs in test and measurement.
Previously, he was manager of RF design at Bird Electronics, where he led a team of RF designers in creating new and innovative products. Prior to that, he worked for Motorola Component Products Group and was responsible for the design of ceramic comb-line filters for communications devices. Brian graduated from the University of New Mexico, has 40 years of RF design experience, and has authored three U.S. patents.