Performing In-Circuit Inductor and Transformer Measurements in SMPS
Download this article in PDF format.
In switched-mode power supplies (SMPS), magnetic components, namely inductors and transformers, play critical roles. Much of the SMPS design process relies on component specifications and simulation models. However, due to actual signal conditions, parasitics, temperature, and other environmental factors affecting magnetic components’ performance, a power supply may not perform exactly as predicted by specs and simulations. As a result, in-circuit measurements of inductors and transformers under operating conditions are critical to ensuring reliable real-world performance.
With the right tools on hand, making these measurements doesn’t have to be difficult or time-consuming. We’ll first review the basic theory of inductors and transformers, especially as it relates to in-circuit measurements. We’ll then walk through the use of oscilloscope and probes during power-supply operation, and explore the use of induction measurements and B-H curves to gain performance insight.
Inductor Theory
Faraday’s and Lentz’s laws tell us that the current through an inductor and the voltage across the inductor are related as:
This shows that inductance can be thought of as the extent to which a changing current results in an opposing voltage. By integrating, rearranging, and ignoring the sign, we can get:
This reveals that inductance may be determined as a function of voltage and current over time. Such a time-domain measurement is best accomplished using an oscilloscope equipped with a voltage probe, current probe, and the ability to perform integration and plot X versus Y.
In contrast to a theoretical inductor, the inductance value of a real inductor depends on current levels, temperature, and frequency of operation. In a power supply, these characteristics vary in real time with operating conditions.
1. A basic inductor is a coil wound on a closed ferromagnetic core. Current of I amperes flows through the coil, which has N turns. The inductance of the coil describes the relationship between the current flowing in the coil and the magnetic flux.
As an example, the inductance of the toroid in Figure 1 may be approximated by:
where µ is magnetic permeability of the core; N is the number of turns of wire on the toroid; r is the radius of the core from the dashed center-line in cm; and A is the cross-sectional area of the core in cm2 (assumed to be small relative to the radius of the toroid).
Since this number of turns is squared, it’s the biggest contributor to inductance. Furthermore, the permeability of the core material plays a significant role. However, the value of the inductance is also related to the physical size of the component. To minimize the size of the inductor, most inductors in electronics use core materials that have a much higher permeability than air.
In short, the characteristics of the core material and geometry are critical in determining inductance over various operating conditions, as well as power loss in the device.
Inductance Measurements
Power-supply designers typically use simulation techniques to determine the appropriate inductor value for a design. After manufacturing the inductor, a common practice is to verify the inductance using an LCR meter. However, most LCR meters stimulate the component with sinusoids over a narrow frequency range, so while this is a good technique for confirming that the component is roughly the correct value, it’s a poor predicter of in-circuit performance.
The inductance characteristics of an inductor depend on the current and voltage source excitation signal, wave shape, and frequency of operation, which may vary in real-time operating conditions. Therefore, it’s important to measure and observe the behavior of an inductor in the dynamically changing environment of the power supply.
These measurements are made by probing the voltage across the device, usually with a differential voltage probe. A current probe is typically used to measure the current through the magnetic component. To determine inductance, scope-based power-analysis software integrates the voltage over time and divides by the change in current. It also removes any dc offset and uses averaging to calculate the inductance value.
When measuring a transformer’s inductance, it’s important to avoid loading the secondary winding. Measuring inductance at the primary winding under a no-load condition is equivalent to measuring the inductance for a single-winding inductor. When you’re measuring the inductance of the coupled inductor with multiple windings on the same core, the measured value of the inductance will deviate from the actual value, due to the influence of the current on the other winding(s).
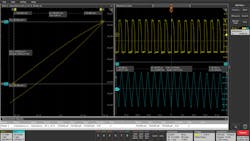
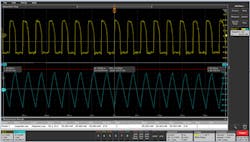
In Figure 2, the inductance measurement gives the average inductance value in henries. The yellow waveform (CH1) is the voltage across the inductor and the blue waveform (CH2) is the current through the inductor. The plot on the left shows current, i versus ∫vdt, the slope of which is inductance.
2. Average inductance value in henries.
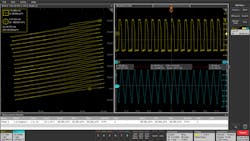
Figure 3 shows the I vs. ∫V measurement, which provides additional insight on inductor performance. Here you can see any dc bias as it builds up over multiple cycles. The yellow waveform (CH1) is the voltage across the inductor and the blue waveform (CH2) is the current through the inductor.
3. This shows the I vs. ∫V measurement, which provides additional insight on inductor performance. Here you can see any dc bias as it builds up over multiple cycles. The yellow waveform (CH1) is the voltage across the inductor and the blue waveform (CH2) is the current through the inductor.
B-H Curve Measurements
Magnetic power-supply components are designed for expected operating voltage, current, topology, and the particular type of power converter. The operating regions of inductors and transformers help determine the stability of a SMPS. However, power-supply operating characteristics can vary during power-on, steady-state operation, load changes, and environmental changes, making it extremely difficult to consider all possible scenarios during the design process.
To ensure the stability of the power supply, it’s important to characterize the operating region of a magnetic component in the SMPS. Generally, the goal is to avoid saturation and operate in the linear region of the hysteresis curve. However, it’s extremely difficult to design a magnetic component and ensure that it will operate in a linear region under all conditions.
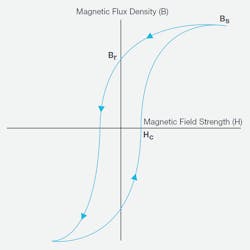
4. Manufacturers of core material may provide such a hysteresis curve as part of their specifications.
B-H curves like the one shown in Figure 4 help designers visualize the performance of an inductor and its core. In this example, H, measured in A/m, is the magnetizing force in the device. It’s measured in amperes/meter and is proportional to the current:
The resulting flux density, B, is proportional to the integral of the voltage across the device. Magnetic flux density B, measured in units of Tesla, is the strength of the magnetic field. It determines the force that’s exerted upon a moving charge by the magnetic field.
This curve offers a number of important insights, including:
- Permeability, µ. Measured in H/m. This is a characteristic of the core material, and it’s the rate at which magnetizing force H (driven by current) produces flux density B (integrated voltage). It’s the slope of the B-H curve. Designers use high-permeability material to enable physically smaller inductors and transformers.
- Saturation flux density. The point at which additional magnetizing force, H, stops producing incremental flux density, B. Designers avoid saturation in most power-supply applications.
- Hysteresis characteristics. Hysteresis is the “width” of the curve and indicates loss in power supplies. Most designs seek to use magnetically “soft” core materials to minimize Remanence Br, the magnetic flux density that remains in the material after the magnetizing force, H, drops to zero and coercive force, or coercivity c, the value of H required to drive the flux density, B, to zero.
Indications of potential instability include:
- Measured peak flux density close to the saturation flux density specified by the core datasheet indicates that the component is getting close to the saturation.
- BH curves that change from cycle to cycle, indicating saturation. In a stable/efficient power supply, the BH curve will have a symmetrical return path and will trace this path consistently.
An oscilloscope can be used to perform an in-circuit measurement of voltage across, and current through, the winding of an inductor. Given the number of turns in the device, the magnetic length of the device, and the cross-sectional area of the core, it’s possible to derive the actual B and H values based on real- time voltage and current measurements using an oscilloscope.
To generate a B-H plot, you need to measure the voltage across the magnetic element and the current flowing through it. In the case of a transformer, the currents through the primary as well as secondary windings are of interest. A high-voltage differential probe is connected across the inductor or primary winding of the transformer. A current probe measures the current through the inductor or primary. Current probes are also used to measure the current through the secondary windings, if needed.
Figure 5 shows the magnetic measurements on a multi secondary winding transformer. The Ref1 (white) waveform is the voltage across the inductor and the Ref 2 (blue) waveform is the inductor current. In this case, the math wfm (orange), which is the resultant current wfm, shows up because the scope was set up to test multiple secondary windings.
5. This shows magnetic measurements on multiple secondary winding transformers.
B-H Curves for Transformers
To measure the magnetic characteristics of a transformer under operating conditions, care must be taken to account for current being transferred into the secondary. When measuring the B-H curve on a transformer, it’s helpful to consider a theoretical element call the “magnetizing inductor.”
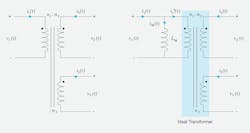
The magnetizing current is the current that would flow through the primary of the transformer when the secondary is open (unloaded). In other words, the magnetizing current doesn’t produce any current in the secondary. As shown in Figure 6, transformers are modeled with this magnetizing current flowing through a “magnetizing inductor” across the primary. Generally, this is used to model the magnetization characteristics of the core material.
6. In this transformer schematic (left) and equivalent circuit (right), the magnetizing current is flowing through an imaginary inductor, LM, in parallel with the primary. LM models the magnetic characteristics of the transformer.
Loss Analysis
Losses in magnetic components are significant contributors to overall loss in a power supply. Core loss depends on the magnetic properties of the material and includes hysteresis loss and eddy current loss. Copper loss results from the resistance of the windings; it also depends on the load connected to the secondary side of a transformer.
A number of techniques are used to estimate core loss. One more popular technique is the Steinmetz empirical formula, which relates core loss to frequency and flux density:
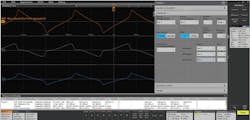
where k, a, and b are constants for the core material, generally taken from the core manufacturer’s datasheet. Datasheets may also give loss estimates at various frequencies and flux densities that are typically given in response to sinusoidal excitation. However, in power applications, components are usually driven with non-sinusoidal stimuli, causing uncertainty in such approximations (Fig. 7).
7. Example of a total magnetic loss measurement.
Scope software can be used to compute total magnetic loss by averaging power of voltage and current waveforms, average (v(t) ∙ i(t)). With this method, the total magnetic loss includes both copper loss and core loss. This is shown Fig. 7, where the magnetic loss measurement gives the total magnetic loss, including core and copper loss. You can find the core loss from the component manufacturer’s datasheet and derive the copper loss by subtracting the core loss from the total magnetic loss.
Scopes are capable of calculating the magnetic loss in a single winding inductor, a multiple winding inductor, or even a transformer. In the case of a single-winding transformer, a differential probe is connected to measure the voltage across the primary winding. A current probe measures the current through the transformer. The power-measurement software can then automatically calculate the magnetic power loss.
Inductors and transformers serve key roles in switch-mode power supplies, including filters, step-up/step-down, isolation, energy storage, and oscillation. Ensuring they perform as expected requires thorough in-circuit measurements performed under operating conditions. As we’ve discussed, modern oscilloscopes equipped with power-analysis software offer fast setups and improved repeatability.
Wilson Lee is Technical Marketing Manager at Tektronix.
