From the Richter scale to sound pressure, many modern units utilize the logarithmic “base 10” system. But to many engineers, the decibel (dB) remains one of the trickiest concepts of test and measurement. RF engineers are known to throw around a wide range of dB terms, including dBm, dBc, dBW, and even plain old dB. Although many of these units might seem confusing, the decibel and all of its variations are actually straightforward.
The “decibel” is defined as one-tenth of a Bel, a unit devised during the early 1920s. The original name for the Bel was the transmission unit (TU). The TU first was used to describe the signal loss that occurred over long distances of telephone cable, which replaced another unit of power loss, the “mile of standard cable” (MSC). The TU was based on a base 10 logarithmic scale and eventually was renamed the Bel in honor of Alexander Graham Bell.
Although some might find the dB (0.1 Bel) to be confusing, it fundamentally is nothing more than a description of a ratio. Moreover, it is a convenient term that allows us to describe extremely large ratios with simple language using a logarithmic scale.
Decibels Versus Linear Ratios
First, let’s evaluate the mathematic ratio between two signals at power level A and power level B. In addition, we can give power level A and power level B real numbers. For example, suppose:
• Power level A = 100 W
• Power level B = 1 W
Given the values of levels A and B, the power ratio between each power level can be described in straightforward language:
• A is 100 times more than B.
• B is one-hundredth (1/100) of A.
Note that common descriptions of ratios such as “100 times” and “hundredths” are descriptions of linear ratios. To convert linear ratios to logarithmic ratios (dB), simply use:
RatioA to B(dB) = 10 log10(A/B) = 10 log10(100 W/1 W) = 20 dB
The language of “100 times” translates directly to 20 dB. Equation 2 describes “one-hundredth” in linear terms:
RatioB to A(dB) = 10 log10(B/A) = 10 log10(1 W/100 W) = –20 dB
Similarly, the language of “hundredth” translates directly to –20 dB. Based on the calculations in Equations 1 and 2, we now can describe the ratio between quantity A and quantity B in logarithmic terms:
• A is 20 dB more than B.
• B is 20 dB less than A.
• B is –20 dB relative to A.
Using logarithmic terms, the sign tells us which quantity is greater.
A Rant About Audio Engineers And Audiologists
Given the simplicity of this explanation, I like to somewhat jokingly blame audio engineers and audiologists (though I like them as people) for confusing RF engineers. Audiologists and others frequently use “dB,” a description of ratio, to describe loudness in absolute terms.
In the audio world, it is perfectly acceptable for someone to say “my neighbors were blasting their music at 90 dB all night long.” But a ratio without a notion of a reference quantity is meaningless. So, describing music at “90 dB” must mean 90 dB louder than something else.
Although audio engineers and audiologists do not explicitly state the reference quantity, it is generally implied that 0-dB sound is considered to be the minimum sound pressure that the human ear can hear. In terms of sound pressure, then, 0 dB is 2 â 10–5 Pa (pascals). For example, a sound at 20 dB (quiet conversation) really means 20 dB above what the human ear can hear, or 2 â 10–4 Pa.
Decibels In RF And Microwaves
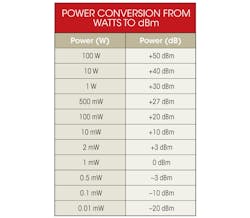
In the RF and microwave community, the notation of the decibel follows the pattern of dBx, where “x” describes the reference unit. Common “dBx” terms include dBV, dBm, dBW, dBc, and dBr. Although “watts” is the reference unit of power of an electromagnetic signal, most engineers prefer to describe power relative to 1 mW, abbreviated simply as dBm. In dBm terms, 0 dBm is equal to 1 mW, and +30 dBm is equal to 1000 mW, or 1 W (see the table).
One important convention is the sign in front of the expression of power. Power levels greater than 0 dBm are always represented with a + in front of the number. Thus, 10 dB above 1 mW is +10 dBm. Note that a difference of 3 dB corresponds to either “half” or “twice” the power, depending on the sign.
Although dBm is arguably the most common unit of power in RF and microwave systems, it’s not the only one. Another common unit is decibels relative to 1 W, or dBW. As the name suggests, 0 dBW would equal 1 W. Any power level expressed in dBW can be converted to dBm simply by adding 30 dB, which is the ratio of 1 W to 1 mW:
Power (dBm) = power (dBW) + 30
While terms like dBm and dBW are common metrics of absolute power, RF and microwave engineers use a wide range of dB terms to describe the power ratio of a range of signals. For example, common dB expressions include dBc, which is dB relative to an arbitrary carrier, and dBr, which is dB relative to an arbitrary power level (usually referenced to a power spectral density plot).
Decibels And The Spectrum Analyzer
A solid understanding of dB and dBm is essential to truly understand the measurements a spectrum analyzer makes, especially as it relates to noise and bandwidth. Fundamentally, spectrum analyzers display power on the Y axis versus frequency on the X axis. One useful mental exercise to test your knowledge of dB is to determine the power of the spectrum analyzer’s noise floor as a function of the integrated bandwidth.
On a spectrum analyzer, the level of the noise floor (on the Y axis) fundamentally depends on the bandwidth in which that power is measured. For example, suppose the spectrum analyzer has a noise floor of –160 dBm/Hz. In this scenario, the “visible noise level” would appear as –160 dBm only when the resolution bandwidth of the spectrum analyzer is set to 1 Hz.
Using our knowledge of the dB scale, we can imagine what the visible noise level would be if the resolution bandwidth was set to 100 Hz instead of 1 Hz. In this case, summing each of the individual 1-Hz bins would produce a noise level that is 100 times higher. Translating our language of “100 times” to dB, the visible noise level in a 100-Hz resolution bandwidth is 20 dB higher. A spectrum analyzer with a noise floor of –160 dBm/Hz, then, shows a noise level of –140 dBm when configured to a resolution bandwidth 100 Hz. Not that one can typically configure a spectrum analyzer to display power as a “power spectral density,” which normalizes the power displayed on the Y axis to a 1-Hz bandwidth through the exact calculation.
Parting Thoughts
I truly hope I have shed some light on the mystery of the dB and how it relates to descriptions of linear ratios. For more information on interpreting the display of your spectrum analyzer, visit ni.com/rf-academy.
David A. Hall is a senior product marketing manager at National Instruments, where he is responsible for RF and wireless test hardware and software products. His job functions include educating customers on RF test techniques, product management, and developing product demos. His areas of expertise include instrumentation architecture, digital signal processing, and test techniques for cellular and wireless connectivity devices. He holds a bachelor’s degree with honors in computer engineering from Penn State University.
About the Author
David Hall
Head of Semiconductor Marketing
David A. Hall is the head of semiconductor marketing at NI and is responsible for developing and executing go-to-market plans for the semiconductor industry. His job functions include managing the semiconductor test business, identifying industry trends, and educating customers on best semiconductor test practices. Hall’s areas of expertise include ATE architectures, RF measurement techniques, digital signal processing, and best measurement practices for mobile and wireless connectivity devices.
With nearly 15 years of experience at NI, Hall has served in multiple roles throughout his career including applications engineering, product management, and product marketing for automated test and RF instruments. He has also held management positions in product marketing, which focused on employee development and meeting business results across products and application areas. Hall is a known expert on subjects such as 5G, the Internet of Things (IoT), autonomous vehicles, and software-defined instrumentation. He holds a Bachelor’s with honors in computer engineering from Penn State University.