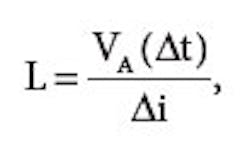Expedite Transformer Calculations for Flybacks
Using a flyback topology to generate a high voltage is a common approach. The voltage can charge a capacitor for a high-energy pulse. Such an approach is used in defibrillator capacitors, photoflash capacitors, strobe capacitors and ignition circuits to name a few. Using a new step-by-step procedure, it's possible to quickly realizeaninitial flyback transformer design for charging a capacitor in a stated amount of time.
Following this procedure eliminates “cut and try” and over-design approaches. It also allows designers to select critical values with confidence, and can be used to provide insight as to the effects of holding an element constant and varying other elements. The variables included are frequency, voltage, pulse width, peak current, load capacitance and efficiency.
Before we delve into this novel approach, we need to understand the pros and cons of flyback topologies. Advantages include circuit simplicity, a high-voltage output that's not dependent on a large transformer turns ratio, a self-limiting circuit that can be short circuited without any damage, and an output that can be regulated over a large range. A flyback also can provide voltage isolation, allows for multiple isolated outputs where one output can be used for a low-ratio feedback voltage, and does not require a smoothing choke.
The disadvantages of flyback topologies include the need for a large and often bulky transformer, a fast-switching output that can generate problematic EMI signals, leakage inductance that must be kept low for good efficiency and a circuit that can be damaged once a load is removed without using a feedback loop.
Fig. 1 shows a simplified circuit and Fig. 2 shows idealized waveforms for a frequency of 50 kHz and a pulse on time (TON) of 45%.
The flyback operates by storing energy on the “charge” portion of the cycle and delivers the stored energy to the load on the discharge cycle. In the case of a flyback, the transformer is often described as a coupled inductor. Due to the diode polarity, current only flows in the secondary side during discharge. During the charge cycle, energy is stored in the primary inductance by a current ramp. The dead time shown in Fig. 2 ensures that the flyback is discontinuous. As the capacitor approaches full charge, the dead time increases.
The primary current ramp (charge) follows the inductance formula:
where L is the inductance in henries, VA is the applied voltage, (Δt) is the time duration from start to finish of the applied pulse and (Δi) is the change in current over the same interval. If i starts at zero, Δi is equal to the peak current (IPEAK):
Eq. 2 is Eq. 1 solved for IPEAK. For example, if VA = 12 V, Δt is 0 µs to 15 µs, L = 60 µH and IPEAK = 3 A.
The energy stored in the inductance is:
where U is energy measured in Joules, L is in henries and IPEAK is in amperes. In the previous example, the energy stored in each pulse is 270 µJ.
It is during the discharge of this stored energy that the greatest advantage of the flyback is realized. The output voltage will rise to whatever level is needed to cause current to flow, thus dissipating the stored energy. The voltage of the output has limits to be sure, but within the insulation structure, transistor breakdown, and circuit design, and taking losses into account, the voltage can rise to very high levels.
Though ancient technology now, the most common example was the flyback transformer in color TVs with a cathode ray tube. These transformers could generate voltages greater than 35,000 V, voltages so high that, when the circuits malfunctioned, the TV could generate damaging X-rays. The analysis is somewhat simplified because the TV flyback transformer performs more functions than just generating high voltage. The design of the flyback circuit and transformer for power transformation is well illustrated in Abraham I. Pressman's book Switching Power Supply Design.[1]
The block in Fig. 1 labeled “pulse control” can take many forms. In a defibrillator, pulse control will be a voltage feedback loop that fixes the number of Joules to be delivered to the patient. During successive resuscitation attempts, the level will increase. For photoflashes, the charge level is fixed. The capacitor will be charged and additional pulses will only be applied as a refresh.
In photoflash applications, the dead time may be limited to speed up the charge time. The low dead time and variable discharge produces the characteristic of an increasing high-pitch sound. Variations in the pulse-control element are almost endless.
Design Example
With the background provided, we can now tackle the problem of charging a capacitor to a given voltage in a stated amount of time. Designs begin with a list of known values.
Let's illustrate the process by considering the following example of a typical design problem, for which the values are listed in the table. The application is for charging a defibrillator capacitor. (Caution: The charged capacitor used in this example can provide a lethal shock.)
The first step is to determine the number of Joules required to charge the capacitor:
where U is energy in Joules, VCAP is the capacitor voltage and C is the capacitance in Farads.
The next step is to calculate the number of charging pulses (N) in the stated time:
In the third step, calculate the energy required per charging pulse (UP):
The fourth step is to make an estimate of the circuit efficiency and include the factor in calculating the energy that must be supplied. All calculations up to this point are based on the assumption that there were no losses in the switching transistor, diode and transformer (winding or core). Switching transistor, diode, and transformer losses are shown to a first order. Second-order losses are those for winding capacitance and leakage inductance.
Fig. 3 provides an estimation of a typical loss factor expressed as an efficiency figure. The losses must be included in the power supplied from the dc source, as shown in the next calculation. Note that Fig. 3 is an estimate and results will vary. Use the result from Eq. 4 (in this case, 200 J) to find the efficiency value. A number of variables in circuit design, layout, transformer design, components and others will affect the result. (For very high-voltage designs, even leakage current paths across the surface of the pc board and leakage within the capacitor must be considered.)
In the fifth and final step, solve for the unknowns. There are two unknowns and two equations previously presented that will provide the answer. The unknowns are the transformer primary inductance and the peak current. The 500-µJ figure calculated in the previous equation can be solved with an almost infinite number of solutions. The remainder of the design requirements and the 500-µJ calculation limits the answer to one solution (as shown next).
Eq. 1 is an inductance formula, while Eq. 3 is solved for the inductance. The right-hand side of both equations are equal to each other. The resulting expression, with only one unknown, can be solved for the peak current. Having found the peak current, the value is entered into the original equation and solved for the inductance. For a “sanity check,” both formulas are solved for the inductance. The equal results provide confidence that the calculations were performed correctly.
Calculate the inductance by substituting the value of IPEAK in both Eq. 1 and Eq. 3 as a check:
Fig. 4 is the completed design with the calculated values included.
A similar application to charging a defibrillator capacitor is charging a photoflash capacitor. Linear Technology's LT3468 IC performs most functions in a small footprint. The IC is designed around the specific application with some other applications mentioned in the data sheet. One limitation of this device is the breakdown voltage of the switching transistor, which at 70 V at 25°C makes it better suited for lower-voltage applications.
The LT3468 data sheet[2] provides design information, circuits and typical waveforms, and gives a designer good insight into the process, possibly sparking new avenues of application. (Note: The data sheet provides a warning related to working with high voltage. Many of the circuits discussed can provide lethal shocks when working properly.)
For further illustration of the design process, the following low-power example was built and tested. Test data, notes on circuit operation and waveform are shown. The design starts with this list of given values:
- C = 6 µF
- V = 600 Vdc
- Charge time = 10 sec
- Circuit = flyback
- Frequency = 50 kHz
- Maximum duty cycle = 45%
- Maximum on time = 9 µs
- Input = 12 Vdc
Using the technique shown previously, the inductance and peak charging current are calculated here:
- Eq. 4 = 1.08 J
- Eq. 5 = 500,000 pulses
- Eq. 6 = 2.16 µJ/pulse
- Eq. 7 = 4.32 µJ/pulse (efficiency is estimated to be 50%)
Calculate the inductance by substituting the value of IPEAK in both Eqs. 1 and 3.
Knowing the nominal primary inductance and the peak current, the design of the transformer can proceed. The transformer design for a flyback circuit does not follow normal transformer design procedures. The flyback transformer can be viewed as two inductors sharing a common core. (Reference 3 given at the end of this article illustrates that selection of a transistor or the turns ratio is the first step. Chapter 7 of the same reference provides general design guidelines. Reference 4 also provides detailed transformer design information.)
The transistor selected for this example is International Rectifier's IRFD220. The drain-to-source breakdown voltage is 200 V. With an output voltage of 600 V and allowing for a margin of 10% below the breakdown voltage (20 V), a minimum of a 60-V switching spike yields 120 V peak. Use of this transistor gives a nominal turns ratio of 600/120 = 5:1.
Selecting a transistor with a high breakdown voltage keeps the turns ratio low, reducing the losses in the switching transistor. Windings are designed to keep leakage inductance and distributed capacitance low with adequate spacing for voltage breakdown without impregnation.
A demonstration transformer was wound with the following design data:
- Core: RM5I/-3F3 with approximately a 0.003-in. gap in the center leg
- Bobbin: RM5 printed-circuit style
- Primary: 60 turns of #31 AWG
- Secondary: 306 turns of #41 AWG (actual ratio = 5.1:1, extra turns completed even layers for low leakage inductance)
The transformer test results included:
- Primary dc resistance 1-3= 0.73Ω
- Secondary dc resistance 4-5 = 36.1Ω
- Primary inductance = 1.305 mH
- Leakage inductance = 5.99 µH
- Distributed capacitance 4-5 = 10.2 pF.
The Fig. 5 circuit is used to test the transformer. The operating frequency was set to 50 kHz by setting the counter to read frequency, holding the discharge switch closed, pressing the start button and adjusting the 1-kΩ potentiometer.
Either the manual or automatic stop must be used to terminate the charge cycle because the output voltage can exceed 600 V and either the capacitor or transistor will fail. Tests using the automatic stop gave an average total pulse count of 415,000. This total pulse count yields a charge time of 8.3 sec. The difference between the result and the design charge time of 10 sec is due to a smaller capacitor (measured at 5.8 µF), a reference diode that was slightly below nominal and, most of all, an efficiency that was better than 50%.
Fig. 6 is the charging waveform. The waveform was made by replacing the output monitor with the 10-MΩ input impedance of a X10 oscilloscope probe. Fig. 7 shows the voltage between the drain lead of the MOSFET and ground just before stop.
When designing a circuit of this type, there are a couple of pitfalls. One is the inherent danger of a high voltage. High voltage requires careful layout with attention to safety. The other common problem with this type of circuit is the storage capacitor itself. Finding a capacitor with low enough leakage at the operating condition can be a difficult task. Capacitor specifications sometimes specify leakage values at one-tenth of the rated voltage. Leakage currents near the full voltage may be many times the given value rather than would be the expected linear change. The capacitor used in the example is a metallized polyester film type.
The information provided will help engineers design capacitor charging circuits. The equations and procedures presented give insight into the interaction of variables. This information can be adapted and used for testing most capacitor charging circuit designs.
References
-
Pressman, Abraham I., Switching Power Supply Design, 2nd Edition, McGraw-Hill, ISBN 0-07-052236-7, 1998.
-
Linear Technology Corp., LT3468 Data sheet, LT/TP0105 IK Rev A, 2003.
-
Pressman, Abraham I., Switching Power Supply Design, Chapter 4.3.2., 2nd Edition, McGraw-Hill, ISBN 0-07-052236-7, 1998.
-
Dixon, Lloyd H. Magnetics Design Handbook, Texas Instruments, 2001.