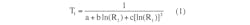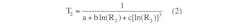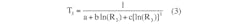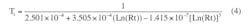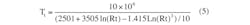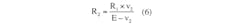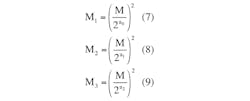Microcontroller Solves Complex Temperature Polynomial Equations
>> Electronic Design Resources
.. >> Library: Article Series
.. .. >> Series: Ideas for Design
.. .. .. >> Ideas for Design Volume 2
When you need to measure temperature using thermistors, you face the challenge of linearizing their response to get accurate readings. One of the best methods for linearizing a thermistor is the polynomial “Steinhart-Hart” equation (S-H), which has an error of 0.1°C. The temperature range for this design is from 0°C to 100°C.
Related Articles
- Software Linearization Techniques For Thermistors
- Thermistors And A Microcontroller Simplify Anemometer Design
- The Real World Versus Your ADC
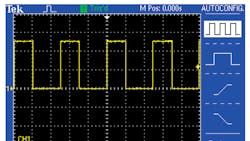
Three thermistor coefficients—a, b, and c—are required to implement the S-H equation. If the manufacturer does not provide the coefficients, you can obtain them by solving the S-H equation (Equations 1, 2, and 3) for three different temperature points. In this design, a PIC MCU will solve such equations to provide accurate readings in 40 ms (Fig. 1).
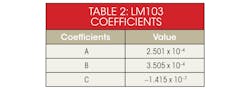
To illustrate, we will use the negative-temperature-coefficient (NTC) LM103 thermistor, which has the resistance at three different temperatures shown in Table 1.
With these three measurements, the temperature is converted to the Kelvin scale and substituted into three Steinhart-Hart equations:
Solving these three equations yields the coefficients a, b, and c (Table 2).
Substituting the coefficients in the Steinhart-Hart equation, we get the thermistor equation:
or:
The challenge for the PIC 16F887 microcontroller is to use Equation 4 to get true temperature readings. This project consumes 1227 words of the microcontroller’s memory. Input AN0 is declared as analog, and the rest of the I/O lines are declared digital outputs. The analog-to-digital converter (ADC) is configured for 10 bits, with a sampling time of 50 µs.
The thermistor’s voltage reading is stored in binary format in the variable “volt” with the instruction ADCIN 0, volt. Then, this reading is multiplied by 48,828 to convert it to decimal, and it is stored in a new variable called “v1.” To obtain each decimal digit from variable “v1,” the commands DIG3, DIG2, and DIG1 are used to store these readings in three variables called dig3, dig2, and dig, respectively.
This file type includes high resolution graphics and schematics when applicable.
The code, available here, shows the software program where the following variables are declared for processing and storing the readings: B, A, C, L, volt, v1, v2, pattern, pattern2, pattern3, I, digit3, digit2, and digit. Two variables (conv1 and conv2) are required for binary-to-decimal conversions. They include the 10-bit resolution ADC’s least significant bit (LSB), which is equal to 4.8828 mV.
The algorithm that was developed to get a temperature reading using the Steinhart-Hart equation requires several steps.
First, compute the power supply voltage (v1), which is equal to 48828 × volt2. Variable volt2 is read with the PIC’s 10-bit ADC. If the power supply is correct, volt2 = %1111111111, and then v1 = 49,951,044. Now with the instruction DIV32, the variable volt2 is divided by 10,000, giving a result equal to 4995, which represents the approximate value of 5 V from the power supply.
Second, the thermistor’s voltage drop is computed with the same process from the first step, but with another analog-to-digital channel. Let’s say we have a reading in the ADC of 2.5 V (adc = 1000000000). The voltage read is then 24,999,936, which is divided by 10 with DIV32 for a result of 2499, which approximates to 2.500 V.
Third, we proceed to find the resistor’s value with:
To achieve that, we store in a variable called “dif” the power’s supply voltage minus the thermistor’s voltage. Then we multiply the thermistor’s voltage by the 10-kΩ fixed resistor, and we apply DIV32 to divide this last product by “dif,” resulting in the thermistor’s resistance value.
Fourth, we now compute the base 2 logarithm from the thermistor’s resistance with Equations 7, 8, and 9:
where a0, a1, and a2 are the next-digit mantissa in base 2.
Next, we find the characteristic a0 or logarithm’s integer with the function NCD, which delivers the most significant bit (MSB) of a number. If we decrement it by 1, we get the base-2 logarithm characteristic. We know, for example, that the base-2 logarithm for number 47 is 5.554 using four significant digits. Thus, NCD (47) = 6, where 47 in binary is 00101111, and the MSB is in the sixth position from left to right. If we decrement it by 1, we get number 5, which is the logarithm’s characteristic.
To get the logarithm, we need the Mantissa (fractions part). To compute it, we need the result of the successive divisions “wu” by 2 (). Nonetheless this operation or process cannot be applied directly, since dividing 47/2 results in 23.5, and we lose the fractions part. (PIC Basic Pro does not work with fractions.) Therefore, to keep the fractions part, we create a special subroutine that performs the following series:
47/2 = 23.5, 23.5/2 = 11.75, 11.75/2 = 5.875, 5.875/2 = 2.9375, 2.9375/2 = 1.46875
When dividing 47/2 = 23, with a remainder of 1, this “1” appears in the first division of the five that will be performed. Therefore, the fraction 1/25 = 0.03125. We cannot work with fractions, though, so instead of dividing by 1 by 2n, we take the number 10,000 as a numerator, and we create a subroutine that computes the denominator depending on the number of division where appears a remainder of 1.
Then, we sum all the results of the divisions. To continue with this example, we have the following five steps:
• 47/2 = 23, with a remainder of 1; this is the first division of 5, 10,000/25 = 312.5 = 312
• 23/2 = 11, with a remainder of 1; this is the second division of 4, 10,000/24 = 625
• 11/2 = 5, with a remainder of 1; 10,000/23 = 1250
• 5/2 = 2, with a remainder of 1; 10,000/22 = 2500
• 2/2=1, with a remainder of 0; there is no portion to add
In this case the variable “Ja” is equal to 4687, and it still needs to be incremented by one. Therefore, we divide “ja” by 1000 and then we add up 1000. Therefore, Ja = 1468, obtaining approximately the original quantity mentioned above, multiplied by 1000 with four significant digits.
Once we have obtained M, we need to get the mantissa using the process described in Figure 1. The division by 2an is not complicated because we are working in base 2, and the division is performed by 20 or 21. When raising to the square power, we must account for where we will multiply Ma by Ma, and then we use that division by 1000 with DIV32 because the result is greater than 16 bits.
After this process is performed a required number of times, we need to convert an to a decimal base. To achieve this, we multiply by the respective weight, 5, 25, 125, and so on sequentially. And because we cannot work with fractions, we multiply by 5000, 2500, etc.
Finally, we add all the elements to the Mantissa an in decimal format and divide the sum of all of them by 10. We sum a0 × 1000 and we save it in variable “l2,” so “l2” stores the value of the logarithm in base 2 of the thermistor’s impedance. The last step to obtain the natural logarithm is to apply the equation shown below to change its base:
log2x (ln2) = ln x
We know that ln(2)= 0.6931, so we just need to multiply “l2” by 6931 and then divide it by 10,000 using the DIV32 command to store it in variable “lm,” which is the natural logarithm of the resistor multiplied by 1000.
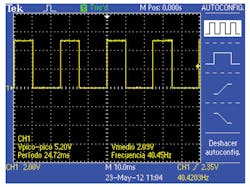
To drive the common pin of the LCD, a for-next loop enables the output RC2 to be “1” (Fig. 2).
Then the subroutine “D” is invoked to convert the decimal data to a seven-segment code. The LOOKUP function decodes the decimal value of digit3 to a seven-segment format that is stored in variable pattern3. Now the value of RC2 (stored as a byte in variable L) is XORED with pattern3 to drive the LCD in phase.
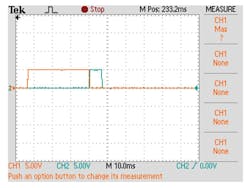
This process is repeated with the other two digits while a 10-ms pause is added. Then, RC2 is turned off and stored as a byte in variable L. Subroutine D is invoked again and the process is repeated with the phase output (RC2) changed for another 10 ms. After every LOOKUP function, every pin is assigned to the corresponding port’s pin dedicated to drive each LCD segment. Total time required is 40 ms (Fig. 3).
Reference
Computing Logarithms Digit-by-Digit, Mayer Goldberg, BRICS RS-04-17. ISSN: 0909-0878
About the Author
Ricardo Jimenez
Ricardo Jimenez holds a master's degree in electronics from the Instituto Tecnologico de Mexicali.
Roberto Solorio
Roberto C. Solorio holds a BS in electronics from the Instituto de Tecnologico de Mexicali.