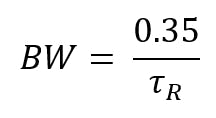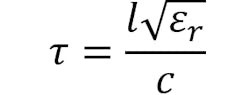Why Skew-Matched Coaxial Cables Matter to Signal-Integrity Test and Measurement
Download this article in PDF format.
This article appeared in Microwaves & RF and has been published here with permission.
Phase stability means reliable performance in specific test-and-measurement applications that call for a close match in frequency and phase between cables with low relative drift over temperature, vibration, and flexure. Yet, phase stability may not be adequate in cases where tighter skew tolerances are needed for a more synchronized distributed clock chain.
Skew-matched coaxial cables are specifically designed to service the growing data-rate demand in differential signaling applications. This article explores some common measurement parameters and how skew-matched coaxial assemblies can augment a test setup to lend more accuracy to the overall differential-signal characterization process.
High-Speed Differential-Signal Device Characterization
Differential signaling is often used in high-speed digital (multi-gigabit) applications because any noise will equally affect both lines if they’re coupled closely together (with adequate conductor width for desired differential impedance). Thus, it’s often much easier to filter noise than in single-ended lines and may reduce transmit-power requirements on the transmission lines.
The common-mode noise introduced by non-ideal devices can be rejected at the receiver. There is, however, cross-mode conversion (common-to-differential mode, differential-to-common mode) that invariably results from manufacturing imperfections that cause device asymmetries. As with any design, prototype, and testing process, all electrical anomalies must be adequately discerned and evaluated before production. While signal-integrity (SI) engineers have numerous tools at their disposal to characterize a differential device, mixed-mode S-parameters are among the more basic and necessary tools for understanding high-speed differential systems.
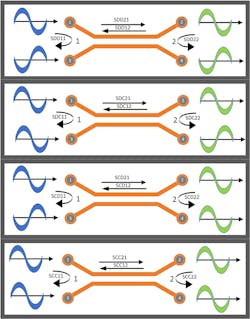
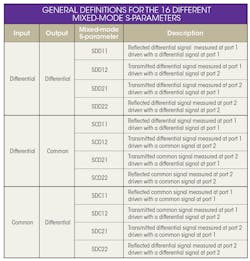
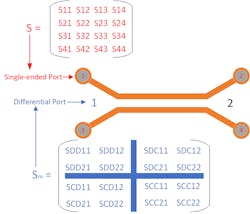
Typically measured with a vector network analyzer (VNA), S-parameters are an extremely useful modeling and measurement tool for the design and analysis of both single-ended unbalanced and differential balanced passive high-frequency systems. However, a single-ended, two-port device under test (DUT) in RF applications would require a 2×2 S-parameter matrix for analysis, whereas a two-port differential DUT would leverage a 4×4 S-parameter matrix. Figure 1 depicts the various mixed-mode S-parameters based on a common/differential input or output.Two-port, single-ended S-parameters reveal insertion loss/attenuation/gain data (S21) as well as return loss/voltage standing-wave ratio (VSWR) data (S11). Differential S-parameters offer insight into the performance of a system with differential return loss (e.g., SDD11), insertion loss (e.g., SDD21), near-end crosstalk (NEXT) (SDD31, SCC31, SCD31), far-end crosstalk (FEXT)(SDD41, SCC41), and differential-to-common mode conversion (SCDxx). The table provides general definitions for the 16 different mixed-mode S-parameters while Figure 2 illuminates some more specific parameters utilized in a mixed-mode analysis.
Time-domain transmission (TDDxx) parameters are also vital in the characterization process, particularly for jitter analysis (eye diagrams) and crosstalk. Multi-domain test templates are popular for testing multi-gigabit digital standards such as USB 3.0, Ethernet, and serializer/deserializer (SERDES) applications.
It’s important to note that a single-ended NxN S-parameter matrix isn’t directly related to the mixed-mode NxN S-parameter matrix (Fig. 3). Aside from using a mixed-mode VNA kit, the mixed-mode S-parameters can be derived mathematically from a traditional VNA Touchstone (SnP) file via adequate mode-conversion matrices.1
Time-Domain Analysis (Jitter, Bit Error Rate)
Time domain analysis can either be performed with an oscilloscope (in TDR mode), a bit-error-rate tester (BERT), or a VNA that performs an inverse discrete Fourier transform (DFT) to convert from the frequency domain (SDD21) to the time domain (TDD21). Where mixed-mode S-parameters are useful for characterizing a differential channel in the frequency domain (crosstalk, noise, insertion loss, and so on), eye diagrams are useful tools in evaluating clock jitter or the BER of the signal; these reveal jitter, interference, and signal attenuation problems. Other time-domain tools, such as single-pulse response, can reveal intersymbol interference (ISI), or the interference of a symbol on a subsequent chain of symbols, which is often caused by clock jitter, noise, and crosstalk.
Jitter testing is of particular importance as data rates and clock frequencies rise, causing eye openings to shrink and leaving far less room for noise, crosstalk, and the various manufacturing flaws that cause jitter. Moreover, shorter rise/fall times, in turn, increase the amount of high-frequency spectral content so that there’s still often considerable energy up to the fifth harmonic. For instance, a 20-Gb/s data rate would correlate to a 10-GHz clock frequency, which would require a bandwidth (BW) of 50 GHz to reveal fifth-harmonic content (and thus increase the resolution in the time domain).
For exceptionally high data-rate applications, the equation for bandwidth (Equation 1) frequently enables successful recreation of the rising/falling edge of the signal. This significantly reduces the bandwidth and dynamic range requirements for test equipment.
where BW is bandwidth, and τR is rise time.
In these cases, a VNA can become an all-in-one tool for multi-domain analysis and more straightforward channel characterization. However, utilizing precision coaxial components, particularly skew-matched coaxial sets with an adequate method for eliminating the errors caused by the test fixtures, increases the likelihood of obtaining the most accurate measurements that the test equipment is capable of.
Use Cases for Delay-Matched Coax Cables
Modern high-speed digital communication systems rely on the precise timing of signals to and from a transmitter or receiver. Examples include SERDES for high-speed I/O signal transmission as well as generalized differential measurements found in high-speed interfaces such as USB 3.1, multi-gigabit Ethernet, and PCI Express.
Measuring channel signal integrity
Generating timing margins is often done at the design and simulation level by characterizing the crosstalk, jitter, skew, and electromagnetic simulation of “flight time” (interconnect delays). However, physical measurements using test instruments may also be necessary to gain a more accurate assessment of channel loss. Flaws, or “pathologies,” within the system can carefully be revealed for better design and margin optimization.
Test benches naturally require the use of additional test fixtures and cables/connectors to reach the test equipment. If these additional components have poor signal-integrity (SI) characteristics, it can convolute the process of isolating the source(s) of jitter, skew, or crosstalk. Such problems are typically only discerned by introducing structures with good SI qualities. This includes the use of skew-matched cables to mitigate the sources of skew within the differential test system.
Error correction and fixture/cable removal techniques
The IEEE P370 task force’s mission was to create an industry standard for the characterization of high-frequency electrical interconnects up to 50 GHz. This has been realized, to some extent, through a list of recommended practices that prevent inaccurate de-embedding of test fixtures and cabling from the DUT, which in turn leads to inaccurate S-parameter measurements. These inaccurate measurements can unknowingly be distributed where there’s no IEEE standard to check the quality of the S-parameters prior to publishing that data.3
Typical calibration for a single-ended system would require a short, open, load, and (one) thru to bring the measurement plane to the DUT (pre-measurement error correction). In a DUT utilizing differential signaling, the PG370 standard for pre-measurement error correction requires the 2X-thru to be customized to the test fixture (i.e., same PCB panel, layer, layer transitions, PCB orientation, and electrical length). Even with more accurate post-measurement custom proprietary algorithms for de-embedding, test-fixture removal adds error to the measurement, harming timing margins and optimization of the DUT.
The procedure for the S-parameter de-embedding itself relies heavily on the accuracy of the S-parameter behavioral model.5 For instance, time-domain measurements such as jitter characterization can be less consistent across measurements without skew-matched coaxial cables, as jitter metrics can be directly affected by the mismatch in delay between the cable assemblies.
Need for Skew-Matched Coaxial Cables
Often, test fixtures for high-speed, differential components will include short lengths of mini coax or semi-rigid cables that guarantee a level of delay match. However, such cables frequently hinder test capabilities due to inflexibility or the lack of length needed to reach test equipment.
Unfortunately, a simple replacement/extension of two seemingly identical coaxial assemblies of the same length can’t reliably accomplish a skew match down to the order of picoseconds. This remains true even when there’s phase tracking, or a controlled manufacturing with consistent materials, fabrication methods, and temperature conditioning to maintain nearly uniform performance across a production line of coaxial cables. Skew-matched coaxial cables require more intentional care with a precise cut and connector attachment as well as respective testing to achieve high accuracies.
While highly effective and often critically important, phase-stable coaxial cables are more frequently used for single-ended port systems. The problem of delay mismatch is only exacerbated in cases where:
- Measurements are performed at wavelengths up to millimeter waves
- Measurements are performed with longer lengths of skew-matched coax
- Cables undergo semi-frequent flexure for T&M purposes
Considerations in Making Skew-Matched Assemblies
Phase-stable coax
A set of skew-matched coaxial cables must each be individually phase-stable to be able to maintain a delay on the order of picoseconds between the two assemblies. Coaxial cables will invariably exhibit insertion loss (S21) due to intrinsic sources of loss (e.g., dielectric loss tangent, dielectric conduction, metallic losses).
The phase/time delay (related to phase (S21)), on the other hand, intrinsically depends on the physical length of the cable as well as the dielectric constant, or relative permittivity (εr), of the dielectric material, both of which are temperature-dependent (Equation 2). The linear coefficient of thermal expansion (CTE) will generally increase with temperature as the dielectric constant decreases. Cable length is generally fixed by the metallic materials due to its hardness in comparison to the insulating material, so the CTE of the inner and outer conductors is more relevant to understanding the changes in length over temperature.
The design of phase-stable coaxial cables is a science unto itself, with a particular focus on the use of stable dielectric materials. Many of the techniques involve introducing air into the dielectric. Low-density and foamed materials exhibit lower insertion loss and more phase stability over temperature, which boosts the velocity of propagation (Vp) to 75% to 80%. However, such materials provide less overall mechanical strength and a less consistent dielectric constant over the length of the material, which means a balancing act between material strength (elastic modulus) and relative permittivity. Phase stability also increases with less overall mechanical strain on the coax.
Highly phase-stable coaxial cable will often be relatively thin to mitigate the bending forces perpendicular to the cable during flexure. Moreover, strain-relief boots are typically added between the connector and the transmission line to buffer the forces from a hard connector ferrule and the softer coax during a bend (Fig. 4). To maintain phase tracking over a lot of phase-stable cables, temperature conditioning or aging mitigates the risk of a divergence in phase during temperature fluctuations over the operational lifetime of the coax.
Making two nearly “identical” cables
Creating a pair of cables that experience near-identical delays means maintaining similar Vp values between the two dielectric materials and adjusting length for the minor (1 to 2%) variations between them. This, naturally, gets trickier as cables grow longer, because greater length widens the window for variations between the two cables. The dielectric constant also decreases with increasing frequency.
Millimeter-wave, skew-matched pairs have a much wider bandwidth to closely match dielectric-constant behavior and thus time delay. The precision of a delay- or skew-matched pair of coax depends on the quality of the cut, attachment of the connectors, and the care put into optimizing each individual set for phase stability. Most importantly, batch testing likely would not suffice for consistently achieving a channel-to-channel delay match of, say, 1 to 5 ps. Each set of cables must therefore be 100% tested for reliable performance across a production line of skew-matched coax.
Conclusion
Skew-matched cable assemblies are particularly useful in characterization of high-data-rate, differential-signaling applications. Along with the large repertoire of test equipment, probes, and fixtures, the passive transmission lines connected to the test equipment can either add to or remove from the integrity of a test setup. Significant design considerations are necessary to ensure a tight skew match between two coaxial transmission lines, thus making channel-to-channel delay matching less straightforward than it may seem.
Steve Ellis is Senior Product Manager at Fairview Microwave.
References
1. Zhurbenko, Vitaliy. Advanced Microwave Circuits and Systems. 2010.
2. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=7407194
3. DesignCon2017 Presentation: Al Neves, Tim Wang Lee, Jack Carrel, Hong-Ahn, Heidi Barnes, Mike Resso: “32 to 56 Gbps Serial Link Analysis and Optimization Methods for Pathological Channels.”
4. DesignCon 2014: “De-Mystifying the 28 Gb/s PCB Channel: Design to Measurement”
5. https://www.microwavejournal.com/articles/31900-understanding-skew-and-delay-matched-coaxial-cablesAbout the Author
Steve Ellis
Senior Product Manager, Fairview Microwave
Steve Ellis, senior product manager for RF interconnects at Fairview Microwave, has been involved in the RF and microwave industry for over 35 years, including extensive work in the areas of microwave component test and measurement and radar and communication systems. He currently oversees the development and growth of Fairview Microwave’s line of RF, microwave, and millimeter-wave interconnect products.