How to Design Very Wide Loop BW High-Performance PLL Frequency Synthesizers (Part 3)

As discussed in Parts 1 and 2, and recapped here, modern wireless communications systems (mainly superheterodyne radio transceivers) are now required to deliver higher performance than ever before, thus placing greater demands on the frequency sources for these systems. Such systems are moving higher in frequency (millimeter-wave, or mmWave, and possibly THz regions), tuning wider bandwidths (BWs), processing more complex waveforms using more elaborate modulation schemes and operating in fast tuning modes.

This is happening in both the commercial and military arenas, Examples include satellite communications and repeaters, terrestrial wireless systems such as the present 5G^15,16 and eventually 6G^17,18 protocols, and tactical line-of-sight radios, among others. Therefore, the frequency sources, and particularly the local oscillators (LOs) for these systems, must also move commensurately higher in frequency and deliver higher performance in terms of low phase noise (our priority interest), low spurious, and fast tuning speed.

In some cases, LOs using direct (MMD) synthesizers are needed to achieve this performance, but they’re usually not lowest in SWAP, cost, and complexity. However, in many cases, LOs using indirect (PLL) synthesizers can be used with excellent results, rivaling the performance of direct synthesizers. They’re usually lowest in SWaP, cost, and complexity, which is our thesis here.

For our case of PLL synthesizers and concerning our priority interest in low phase noise, this means that for the relevant PLLs, as their operating frequencies become higher, their loop BWs must become commensurately wider (i.e., fractional loop BW is the ultimate interest) to achieve low phase noise. By applying the special technique shown here, it’s possible to achieve very wide loop BWs in such synthesizers, which can’t be achieved by conventional methods.

By “relevant PLLs,” we mean those PLLs comprising the synthesizer that significantly influence the operating band phase noise. For multiple PLL systems, this usually is the output PLL, which is normally the highest frequency PLL. For single PLL systems, the situation is obvious.

In addition to the use of very wide loop BWs, using unity closed-loop (CL) gain along with only internal (within any relevant PLL) multiplication also assists in achieving low phase noise. The technique is applied here to an example synthesizer that’s a single loop (thereby having only one relevant PLL, simplifying the situation), Type 2 - 2nd Order system with a 1st Order active proportional-Integral (PI) loop filter, which is used as an LO in an actual working and fielded high-performance receiver.

This topology is widely employed, so the technique has broad applicability. It can also be applied to PLLs using other topologies with appropriate modifications. However, we will restrict our discussion to the topology of our example mentioned above. Moreover, the example synthesizer is based on analog hardware because of the high-frequency loop dynamics involved, rather than digital (or computed) hardware/software approaches, which are limited by present-day computing speeds.

Parts 1 and 2 of this series described the technique, presented the example synthesizer, and discussed the synthesizer general design approach and detailed design, which incorporates the technique. In Part 3, we model and simulate the synthesizer PLL section loop dynamics and measure its critical characteristics, which demonstrates the excellent performance achieved using the technique.

Modeling and Simulation of PLL Section Loop Dynamics

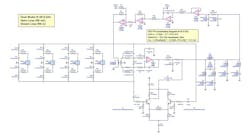
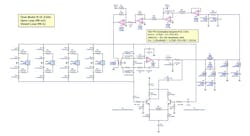
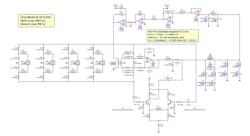
Modeling the single-loop PLL section was a little tricky, since specific PLL simulators aren’t flexible enough to accommodate the more complex loop filter topology of this particular loop. Therefore, a general frequency-domain simulator (Genesys from Keysight Technologies, PathWave Design Division) was used to model the loop in its locked (linear) condition.

There are three specific-case models of the general model along with their OL and CL simulations — the first at the high-band edge of 39.9 GHz, the second at the mid-band frequency of 31.3 GHz, and the third at the low-band edge of 22.5 GHz — for a reasonable sampling of the loop over its operating band.

Each specific-case model (Figs. 1, 2, and 3) begins with the 400-MHz reference baseband input (Port_3) and FB baseband input (A7) to the PFD (A6), which are processed through to its up/down outputs modeled as a differential pair by the secondary of the 1:1 balun (T1).

It should be mentioned that the actual PFD up/down outputs aren’t a differential pair. Rather, they operate independently of each other, only one at a time, with their control voltages moving in the same direction, providing VCO up/down frequency control when combined in the loop filter (A8 and Q1-Q2). However, this is of no consequence — only the relative differential control voltage input to the loop filter (like the model of the secondary of the 1:1 balun) matters, since the effect is the same at the loop filter output.

Then each side of the 1:1 balun secondary shows two parallel resistors of 200 W (R67 and R68) and 68 W (R5 and R8), providing an effective 50-W source for each side of the 1st Order dual-path active PI loop filter (A8 and Q1-Q2). This is of no importance for the op-amp integral amplifier (A8), but it’s of much importance for the differential proportional amplifier (Q1-Q2). The combination represents the PFD internal 200-W output-buffer collector resistor paralleled with an external 68-W collector resistor to the external +5-V supply.

These 50-W sources then feed the PFD gain control (SPDT_1 to SPDT_4) that drives the loop filter feeding the PFD reference/sub-harmonic filter (LC network), which finally drives the VCO control input (RC network and A10). Each model then ends with the VCO-PFD combination integrator (R44, C18 and A9, through the relation RC = 1/ K_fK_v) (Ref. 5) output (Port_4). OL and CL simulations differ by exclusion or inclusion of the FB resistor (R6), respectively.

Each model has three parts that change with operating frequency:

• VCO varicap(s) represented by C42
• VCO K_v represented by C18
• PFD gain control represented by SPDT_1 to SPDT_4

The negative effect of the VCO’s varying K_v (decreasing with increasing frequency) is compensated by the positive effect of the PFD gain control. This, along with the PFD itself, produces an effective oppositely varying K_f (increasing with increasing frequency) to keep the OL gain (proportional to the K_fK_v product) constant across the operating band. The specific-case models, with the modified circuit values noted, accurately represented the loop dynamics at those operating frequencies and performance across the rest of the band was similar.

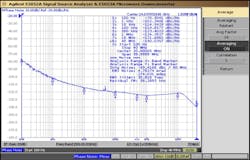
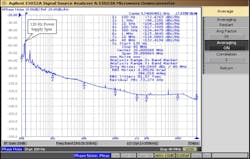
Looking at the OL simulations (Figs. 4, 5, and 6), we see the very high DC (approximated by the 1-Hz frequency point) gain of about 10^13.5 or 270 dB, which is basically due to the high DC gains of the loop filter and VCO. In addition, important frequency points are seen, as are the stability margins, which meet specifications by reasonable amounts.

Then, looking at the CL simulations (Figs. 7, 8, and 9), unity gain and other important frequency points are seen. This is especially the case with the peak frequency, f_peak, showing peaking of < 2 dB, which is good and correlates well with the good stability margins in the OL simulations.

Finally, on both the OL and CL plots, the all-important very wide loop BW of 15 MHz is seen, which is, of course, achieved using the special technique. The general model isn’t perfect, but comes fairly close, is a good starting point, and, with adjusted circuit values, accurately represents performance of the actual synthesizer (EDM unit). The three specific-case models of the general model show the final circuit values used in the actual synthesizer, with some minor adjustments to the OL gain to match model and actual synthesizer due to unavoidable discrepancies encountered.

EDM Measurements and Performance

The performance measurements obtained on the EDM unit — RF line output power, SSB phase noise, spurious, and tuning speed — are important for any synthesizer used as an LO to deliver clean RF power to a converter in a superheterodyne transceiver.

It was felt that baseband loop dynamics measurements of our single-loop system weren’t really necessary because they’re embodied and evident in these results. They could have been done with special instrumentation, though. The measurements are at approximately +25ºC case temperature.

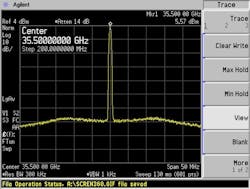
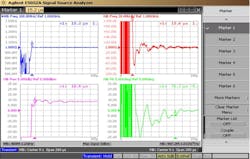
Figures 10 and 11 show typical low- and high-frequency RF line outputs exhibiting good stability with peaking of < 2 dB (spectrum analyzer power readings shown don’t factor in cable losses; however, line powers were also measured with a power meter and fell within the power window specification of +12 ±4 dBm with margin).

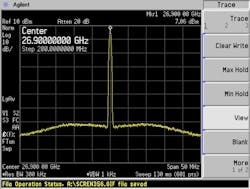
Figures 12 and 13 show typical low- and high-frequency SSB phase-noise performance (our priority interest). As can be seen, it easily exceeds the specification of 350 mdeg integrated over the 100-Hz to 40-MHz offset band by a significant margin, where the very wide 150-MHz loop BW of our single-loop system is quite evident due to the use of the special technique.

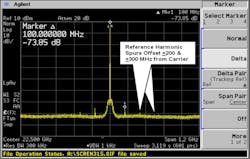
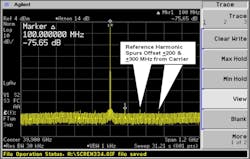
Figures 14 and 15 show typical low- and high-frequency 400-MHz reference and subharmonic spurious exceeding the −60 dBc specification by a significant margin.

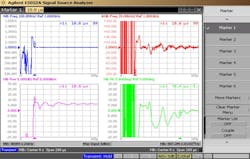
Finally, Figures 16 and 17 show typical tuning speed under worst-case conditions of tuning between the operating band edges in both directions. It exceeds the specification of < 25 ms to within the frequency offset of < 100 kHz and to within the output power window of +12 ±4 dBm (signal source analyzer power readings shown don’t factor in cable losses) with reasonable margin. Although the plots show phase response, there was no phase offset specification.

Conclusion

As we’ve learned, modern wireless communications systems (mainly superheterodyne radio transceivers) are now required to deliver higher performance than ever before. This, of course, has translated to higher performance requirements of the frequency sources, and especially the LOs, for these systems.

We discussed an example of this situation and described a high-performance single-loop indirect (PLL) synthesizer used as a frequency source, and particularly as an LO, in a modern high frequency, wideband, complex demodulation, fast tuning wireless communications system (specifically, a high-performance receiver). The system uses a special technique to produce a very wide loop BW of 15 MHz (with the possibility of pushing this to perhaps 100 MHz or more, if ever practically needed) to deliver very low phase noise for the LO and, ultimately, for the receiver.

Though the direct (MMD) approach can deliver the best performance, the indirect approach, employing this special technique, can be a good alternative. It comes close in performance to the direct approach while offering reduced SWaP, cost, and complexity.

Our example single-loop PLL synthesizer was designed, built (as an EDM unit), developed and tested, and used as an LO in an actual working and fielded high-performance receiver. We described its application and specifications, general design approach, detailed design, and modeling and simulation of loop dynamics, along with measurements and performance. These measurements were then presented showing the excellent performance of the synthesizer, especially with regard to our priority interest in achieving very low phase noise.

It’s believed that this technique will become more prevalent in both the military and commercial arenas as modern wireless communications systems achieve higher performance in terms of higher frequency operation, tuning wider BWs, processing more complex waveforms using more elaborate modulation schemes, and operating in fast tuning modes.

Acknowledgements

This three-part series represents the coalescence, organization and technical writing by the author of the work done by a number of top technical professionals with expertise in frequency synthesizers, radio/radar, and communications systems. It particularly represents the work done by a particular staff scientist and subject matter expert in these areas, who initiated the synthesizer concept and original design, and who produced a prototype unit.

It was a pleasure for the author to have worked with and to have exchanged ideas with these professionals and, especially, the staff scientist. It allowed the author to assume leadership of the synthesizer with his own team, thereby adding his own ideas and developing it to its final production condition. This gave the author the ability to write this paper and, in doing so, further solidified and expanded his knowledge of the subject of PLLs and indirect (PLL) synthesizers.

References

1. F.M. Gardner, Phaselock Techniques, 3rd ed., Wiley, Hoboken, NJ, 2005.

2. R. E. Best, Phase-Locked Loops, Design, Simulation and Applications, 6th ed., McGraw-Hill, New York, 2007.

3. P. V. Brennan, Phase-Locked Loops: Principles and Practice, McGraw-Hill, New York, 1996.

4. E. Drucker, “Phase Lock Loops and Frequency Synthesis for Wireless Engineers,” 1997, Frequency Synthesis & Phase-Locked Loop Design, three-day short course, Besser Associates, Mountain View, CA, 1999.

5. B. Nardi, personal communication, Gaithersburg, MD, 2008.

6. A. Harney, “Designing High-Performance Phase-Locked Loops with High-Voltage VCOs,” Analog Dialogue 43-12, Analog Devices, December 2009.

7. R. C. Dorf and R. H. Bishop, Modern Control Systems, 9th ed., Prentice-Hall, Upper Saddle River, NJ, 2001.

8. W. J. Palm, III, Modeling, Analysis, and Control of Dynamic Systems, 2nd ed., Wiley, New York, 2000.

9. G. Ellis, Control System Design Guide, 2nd ed., Academic Press, San Diego, 2000.

10. W. H. Hayward, Introduction to Radio Frequency Design, Prentice-Hall, Englewood Cliffs, NJ, 1982.

11. S. A. Sedra and K. C. Smith, Microelectronic Circuits, 6th ed., Oxford University Press, New York, 2010.

12. Control System Development Using Dynamic Signal Analyzers, Application Note 243-2, Hewlett-Packard Co., Palo Alto, CA, 1984.

13. Motorola Communications Device Data, Data Book, DL136/D, REV 4, Phoenix, AZ, 1995.

14. F.C. Weist, “Phase Locked Loop Basics for Frequency Synthesizer Applications,” 2010, short course presentation (© 2010 by Frederick Weist), Clarksburg, MD, 2010.

15. “What Frequency Bands Will Roll Out the Carpet for an Official 5G Standard?”, Microwaves & RF, Vol. 56, No. 6, June 2017, p. 20.

16. “Navigating the 5G NR Standards,” Microwave Journal, Vol. 61, No. 12, December 2018, p. 72.

17. S. Pongratz, “6G and The Long RF Journey Ahead,” Microwave Journal, ePublishing Online Article, February 2024

18. C.-X. Wang et al., “On the Road to 6G: Visions, Requirements, Key Technologies and Testbeds,” IEEE Communications Surveys & Tutorials, Vol. 25, No. 2, Second Quarter 2023, pp. 905-974.